





|
【連載 統計解析力アップ講座】 演習;実験計画法とタグチメソッド(2) 第1回演習問題の解答と課題
|
●第1回 演習問題1 解答データ解析の鉄則は「まず、グラフを描け!」です。図表1の折れ線グラフを描いてみましょう。 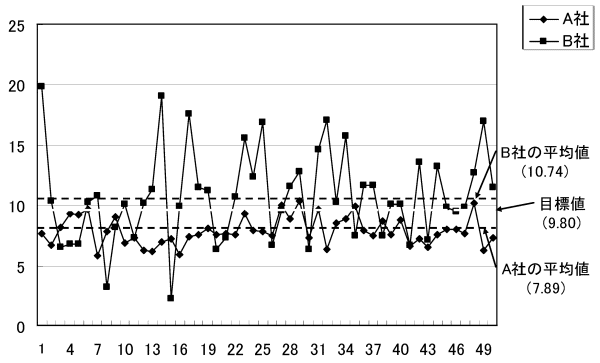
図表3からわかるように、平均値が目標値9.8mmに近いのはB社です。しかしB社の方がばらついています。 ばらつきの指標である標準偏差はA社=1.15、B社=3.82です。 目標値はB社の方が良く、ばらつきはA社の方が良いのです。 目標値とばらつき両方を考慮したものさしが望目特性のSN比です。 望目特性のSN比を求めてみましょう。計算式は、
となります。 式1より、A社、B社のSN比(望目特性)を計算します。 A社のSN比(望目特性):17.38db B社のSN比(望目特性):−3.47db SN比は大きいほど良いので、A社を採用すべきだということがわかります。 ●第1回 演習問題2 解答(1) 図表2の折れ線グラフは図表4のようになります。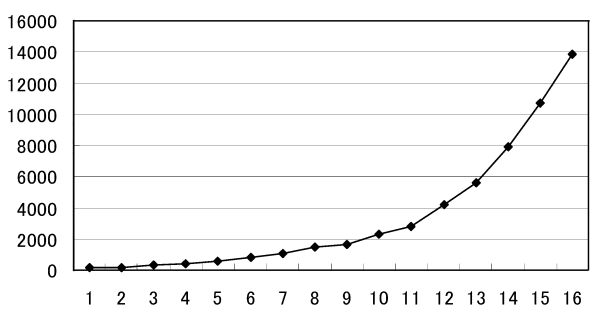
(2) 図表4の折れ線グラフについて多項式(ここでは2次と3次)、指数、累乗、対数の近似曲線を求めます。 Excelのグラフ機能を使うことで求めることができます。
式2、式3、式4、式5、式6に、x=17を代入し、予測値をそれぞれ求め、実測値(16990)との相対誤差を求めます(図表5)。
図表5より、3次式を用いたときの予測精度が一番良いことが分かります。 したがって3次式(y = 9.46 x³−143.11 x²+778.40 x−779.02)が最適な曲線であると判断します。 最適な曲線を求めるための統計的な指標に、選択規準Ruがあります。
Ruを用いて、式2〜6のどれが最適な曲線か判断してみましょう。
図表6より、選択規準Ruの値からも多項式近似(3次)が最適な曲線であることがわかります。 第2回 演習問題図表7はソフトウェア開発時のバグの累積数データです。
最終のバグ累積数はいくらになるか、知りたいですね。 問1 折れ線グラフを描きなさい。 問2 成長曲線:ロジスティック曲線 y = a / (1+be−cx) のa、b、cを求めなさい。 問3 成長曲線:ゴンペルツ曲線 y = ae−bcx のa、b、cを求めなさい。 問4 どちらの成長曲線が当てはまりが良いですか。 問5 最終バグ累積数および収束する週は何週目でしょうか。
|


