| |
 |
問1 図表22の折れ線グラフは図表23です。
図表23 図表22の折れ線グラフ
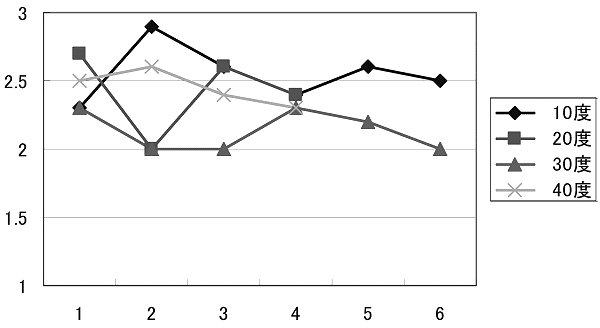
図表23より、10度のとき生成量が最大になりそうであることがわかります。
問2 1元配置のデータから分散分析表を求める公式は次のとおりです。
| 変動要因 |
平方和 |
自由度 |
平均平方(分散) |
F0(分散比) |
P-値 |
F境界値 |
| A |
SA |
a−1 |
SA/(a−1)=VA |
VA/Ve |
(注1) |
(注2) |
| 誤差 |
Se |
a (n−1) |
Se/a(n−1)=Ve |
|
|
|
| 合計 |
ST |
an−1 |
|
|
|
|
(注)繰返し数が水準ごとに異なる場合
n1, n2,・・・, naのときも同様、n1+n2+・・・+na=Nとすれば、誤差の自由度は、N−a、
合計の自由度はN−1となる。
(注1)P−値は、関数FDIST(F,f1,f2)=FDIST(VA/Ve, a−1, a(n−1))を用いる。
(注2)F境界値は関数FINV(F,f1,f2)=FINV(0.05, a−1, a(n−1))を用いる。
|
図表22の分散分析表は図表24です。
図表24 図表22の分散分析表
分散分析表
| 変動要因 |
変動 |
自由度 |
分散 |
観測された分散比 |
P-値 |
F境界値 |
| 温度 |
0.566 |
3 |
0.189 |
4.535 |
0.017 |
3.239 |
| 誤差 |
0.666 |
16 |
0.042 |
|
|
|
| 合計 |
1.232 |
19 |
|
|
|
|
〈分散分析とは〉
全変動を要因である温度による変動と誤差変動に分解します。
要因変動を誤差変動で割り、これを分散比F0とよびます。
分散比F0がF分布に従うことがわかっているので、この値が出現する確率P−値(危険率)を求め、この値が小さい(たとえば5%以下)と要因変動が有意であると判定します。
図表24より、P−値が0.017(1.7%)と小さい値になっています。
つまり温度が生成量の増減に影響をおよぼしていると判断します。
また、Excelの分析ツールを用いて分散分析表を求めることもできます。
操作手順は次のとおりです。
- メニューバーの「ツール」から「分析ツール」を選びます(図表25)。
図表25
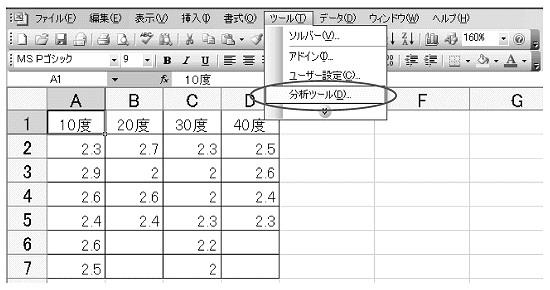
- 「データ分析」ウインドウが表示されます。
「分散分析:一元配置」を選んでOKをクリックします。
図表26 「データ分析」ウインドウ
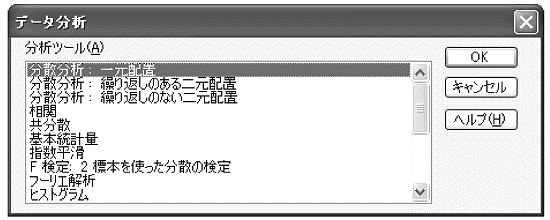
- 図表27のように入力範囲を指定し、ラベルに'をつけOKをクリックします。
図表27
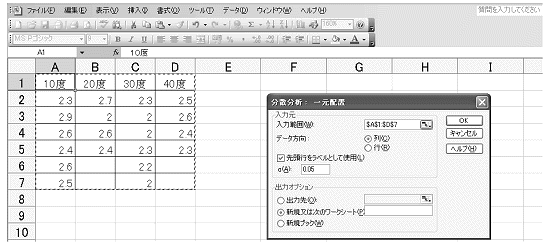
- 出力結果は図表28です。
図表28
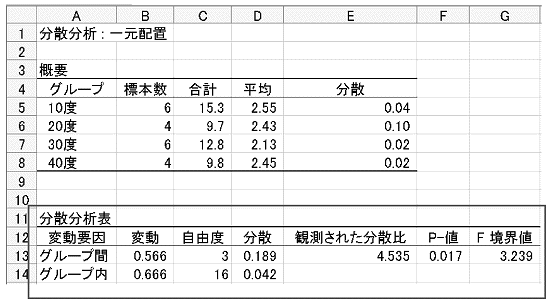
問3 図表22の計画行列は図表29です。
図表29 図表22を計画行列に直したもの
| 温度 |
生成量 |
|
温度 |
生成量 |
| 10度 |
2.3 |
|
30度 |
2.3 |
| 10度 |
2.9 |
|
30度 |
2.0 |
| 10度 |
2.6 |
|
30度 |
2.0 |
| 10度 |
2.4 |
|
30度 |
2.3 |
| 10度 |
2.6 |
|
30度 |
2.2 |
| 10度 |
2.5 |
|
30度 |
2.0 |
| 20度 |
2.7 |
|
40度 |
2.5 |
| 20度 |
2.0 |
|
40度 |
2.6 |
| 20度 |
2.6 |
|
40度 |
2.4 |
| 20度 |
2.4 |
|
40度 |
2.3 |
問4 図表29を0,1データに作り直します。
図表30 図表29を0,1データに作り直したもの
| 10度 |
20度 |
30度 |
40度 |
生成量 |
|
10度 |
20度 |
30度 |
40度 |
生成量 |
| 1 |
0 |
0 |
0 |
2.3 |
|
0 |
0 |
1 |
0 |
2.3 |
| 1 |
0 |
0 |
0 |
2.9 |
|
0 |
0 |
1 |
0 |
2.0 |
| 1 |
0 |
0 |
0 |
2.6 |
|
0 |
0 |
1 |
0 |
2.0 |
| 1 |
0 |
0 |
0 |
2.4 |
|
0 |
0 |
1 |
0 |
2.3 |
| 1 |
0 |
0 |
0 |
2.6 |
|
0 |
0 |
1 |
0 |
2.2 |
| 1 |
0 |
0 |
0 |
2.5 |
|
0 |
0 |
1 |
0 |
2.0 |
| 0 |
1 |
0 |
0 |
2.7 |
|
0 |
0 |
0 |
1 |
2.5 |
| 0 |
1 |
0 |
0 |
2.0 |
|
0 |
0 |
0 |
1 |
2.6 |
| 0 |
1 |
0 |
0 |
2.6 |
|
0 |
0 |
0 |
1 |
2.4 |
| 0 |
1 |
0 |
0 |
2.4 |
|
0 |
0 |
0 |
1 |
2.3 |
〈重要な注意〉
図表30のままでは回帰分析を実行できません。
その理由は、全ての行について、
10度+20度+30度+40度=1
という関係式が成り立つからです。
つまり自由度は4−1=3なのです。
実行するにはいずれかの1列データを削除して自由度を3に
しなければなりません。
(注)自由度とは有効な情報の数のことです。
|
図表30の回帰分析実行結果は図表31です。ここでは30度の列を削除しました。
図表31 回帰分析実行結果
概要
| 回帰統計 |
|
| 重相関 R |
0.677902 |
| 重決定 R2 |
0.459551 |
| 補正 R2 |
0.358217 |
| 標準誤差 |
0.203997 |
| 観測数 |
20 |
分散分析表
| |
自由度 |
変動 |
分散 |
観測された分散比 |
有意 F |
| 回帰 |
3 |
0.566167 |
0.188722 |
4.535002 |
0.017493 |
| 残差 |
16 |
0.665833 |
0.041615 |
|
|
| 合計 |
19 |
1.232 |
|
|
|
| |
係数 |
標準誤差 |
t |
P−値 |
下限 95% |
| 切片 |
2.133333 |
0.083281 |
25.61602 |
2.05E-14 |
1.956785 |
| 10度 |
0.416667 |
0.117777 |
3.537746 |
0.002736 |
0.16699 |
| 20度 |
0.291667 |
0.131679 |
2.214979 |
0.041618 |
0.012519 |
| 40度 |
0.316667 |
0.131679 |
2.404835 |
0.028642 |
0.037519 |
問5
要因である温度が生成量の増減に効いているかは要因選択規準Ruを計算し、
Ru>0
を満たすなら効いていると判定します。
要因選択規準Ruを求める式は、次のとおりです。
【要因選択規準Ruを求める式】
| Ru=1−(1−R²) |
n+k+1 |
・・・式1 |
| n−k−1 |
R:重相関係数
n:データ数
k:水準数−1
|
式1より、
| Ru=1− (1−0.68²) × |
20+3+1 |
=0.189 |
| 20−3−1 |
Ru>0となるので、温度が生成量の増減に影響を及ぼしていると判断します。
問6 図表31より、生成量を求める回帰式は、
| 生成量=2.13+ |
0.42 (A1) |
| 0.29 (A2) |
| 0.00 (A3) |
| 0.32 (A4) |
となります。生成量が最大となるのはA1(10度)のときで、
このとき生成量は
y=2.13+0.42=2.55
と推定することができます。
●演習問題4
繰り返し数が1のときで、2要因実験データを解析しましょう。
図表32は、機械(A社製、B社製、C社製)と温度(10度、20度、30度、40度、50度)の条件下のもと、生成量がいくらになるかを測定した実験データです。
図表32 2要因実験データ
| |
10度 |
20度 |
30度 |
40度 |
50度 |
| A社製 |
83 |
86 |
87 |
85 |
87 |
| B社製 |
80 |
82 |
82 |
86 |
83 |
| C社製 |
79 |
79 |
82 |
83 |
82 |
要因:機械、温度
水準:機械(A社製、B社製、C社製)、
温度(10度、20度、30度、40度、50度)
です。
生成量の増減に機械および温度は効いているでしょうか?
効いているとすれば、どの会社の機械を用いて何度のとき生成量が最大になるでしょうか?
問1 折れ線グラフを描きなさい。
問2 分散分析表を作りなさい。
問3 計画行列を作りなさい。
問4 回帰分析を実行しなさい。
問5 生成量が最大になるときの条件(最適水準)を求めなさい。
|









