| |
 |
問1 図表32の折れ線グラフは図表33です。
図表33 図表32の折れ線グラフ
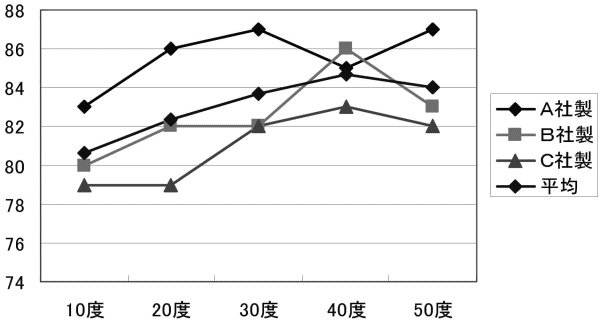
図表33より、機械はA社製、40度のとき生成量が最大になりそうです。このように、実験計画法データは折れ線グラフにすることをお勧めします。
問2 2元配置のデータから分散分析表を求める公式は次のとおりです。
CT(修正項)=(全データの和)²/全データの個数
ST=(個々のデータの2乗の和)−CT
| SA= |
(A1水準でのデータの和)² |
+ |
(A2水準でのデータの和)² |
|
|
| A1水準でのデータの個数 |
A2水準でのデータの個数 |
| |
| + |
────────── |
+ |
(Aa水準でのデータの和)² |
- |
CT |
| Aa水準でのデータの個数 |
SBも同様。A1→B1、a→b、Aa→Bbなどとすればよい。
| SAB= |
(A1B1水準でのデータの和)² |
+ |
(A1B2水準でのデータの和)² |
|
|
| A1B1水準でのデータの個数 |
A1B2水準でのデータの個数 |
| |
| + |
─────────── |
+ |
(AaBb水準でのデータの和)² |
- |
CT |
| AaBb水準でのデータの個数 |
SA×B=SAB-SA-SB
Se=ST-(SA×B+SA+SB)
| 変動要因 |
平方和 |
自由度 |
平均平方(分散) |
F0(分散比) |
P-値 |
F境界値 |
| A |
SA |
a−1 |
SA/(a−1)=VA |
VA/Ve |
(注1) |
(注4) |
| B |
SB |
b−1 |
SB/(b−1)=VB |
VB/Ve |
(注2) |
(注5) |
| A×B |
SA×B |
(a−1)(b−1) |
SA×B/(a−1)(b−1)=VA×B |
VA×B/Ve |
(注3) |
(注6) |
| 誤差 |
Se |
ab(n−1) |
Se/ab(n−1)=Ve |
|
|
|
| 合計 |
ST |
abn−1 |
|
|
|
|
(注1) P-値は関数FDIST (p, f1, f2) =FDIST (VA/Ve, a−1, ab(n−1))を用いる。
(注2) P-値は関数FDIST (VA/Ve, b−1, ab(n−1))を用いる。
(注3) P-値は関数FDIST (VA/Ve, (a−1)(b−1), ab(n−1))を用いる。
(注4) F境界値は関数FINV (0.05, a−1, ab(n−1))を用いる。
(注5) F境界値は関数FINV (0.05, b−1, ab(n−1))を用いる。
(注6) F境界値は関数FINV (0.05, (a−1)(b−1), ab(n−1))を用いる。
|
図表32の分散分析表は図表34です。
図表34 図表32の分散分析表
| 変動要因 |
変動 |
自由度 |
分散 |
観測された分散比 |
P-値 |
F境界値 |
| 機械 |
54.53 |
2 |
27.27 |
15.43 |
0.00 |
4.46 |
| 温度 |
30.27 |
4 |
7.57 |
4.28 |
0.04 |
3.84 |
| 誤差 |
14.13 |
8 |
1.77 |
|
|
|
| 合計 |
98.93 |
14 |
|
|
|
|
機械、温度ともに要因として効いていることがわかります。
また、Excelの分析ツールを用いて分散分析表を求めることもできます。
操作手順は次のとおりです。
- メニューバーの「ツール」から「分析ツール」を選びます(図表35)。
図表35
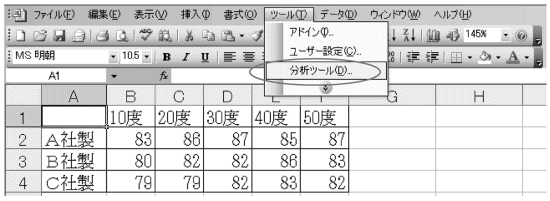
- 「データ分析」ウインドウが表示されます。
「分散分析:繰返しのない二元配置」を選んでOKをクリックします。
図表36 「データ分析」ウインドウ
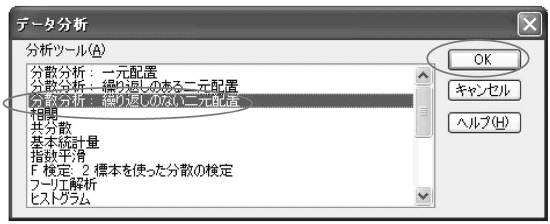
- 図表37のように入力範囲を指定し、ラベルに'をつけOKをクリックします。
図表37
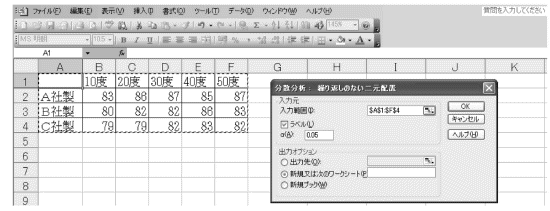
- 出力結果は図表38です。
図表38
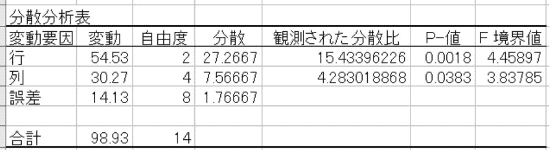
Excelの分散分析表では要因のところを行、列としていることに注意してください。ここでは、行は機械、列は温度のことです。
問3 図表32の計画行列は図表39です。
図表39 図表32の計画行列
| No. |
機械 |
温度 |
生成量 |
|
No. |
機械 |
温度 |
生成量 |
| 1 |
A社製 |
10度 |
83 |
9 |
C社製 |
40度 |
82 |
| 2 |
B社製 |
20度 |
80 |
10 |
A社製 |
50度 |
85 |
| 3 |
C社製 |
30度 |
79 |
11 |
B社製 |
10度 |
86 |
| 4 |
A社製 |
40度 |
86 |
12 |
C社製 |
20度 |
83 |
| 5 |
B社製 |
50度 |
82 |
13 |
A社製 |
30度 |
87 |
| 6 |
C社製 |
10度 |
79 |
14 |
B社製 |
40度 |
83 |
| 7 |
A社製 |
20度 |
87 |
15 |
C社製 |
50度 |
82 |
| 8 |
B社製 |
30度 |
82 |
|
|
|
|
問4 図表39の回帰分析実行用データは図表40です。
図表40 回帰分析実行用データ
| A社製 |
B社製 |
C社製 |
10度 |
20度 |
30度 |
40度 |
50度 |
生成量 |
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
83 |
| 0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
80 |
| 0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
79 |
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
86 |
| 0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
82 |
| 0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
79 |
| 1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
87 |
| 0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
82 |
| 0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
82 |
| 1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
85 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
86 |
| 0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
83 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
87 |
| 0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
83 |
| 0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
82 |
生成量を予測するための最適な回帰式を求めることを考えます。
要因の組み合わせとして次の3通りが考えられます。
(1)「機械、温度」の2要因
(2)「機械」の1要因
(3)「温度」の1要因
(1)〜(3)のうち、どの要因を用いた予測式が最適な予測式なのでしょうか。
要因選択規準Ruを用いて最適な回帰式を求めます。
【要因選択規準Ruを求める式】
| Ru=1−(1−R²) |
n+k+1 |
・・・式1 |
| n−k−1 |
R:重相関係数
n:データ数
k:機械の水準数−1+温度の水準数−1
|
最適な回帰式となるのはRuが正の数でその値が最大となるときの組み合わせです。
図表40をもとに回帰分析を実行します。
図表41 要因を機械と温度とした場合の回帰分析実行結果
概要
| 回帰統計 |
| 重相関R |
0.926 |
| 重決定R2 |
0.857 |
| 補正R2 |
0.750 |
| 標準誤差 |
1.329 |
| 観測数 |
15 |
| Ru= |
0.607 |
|
分散分析表
| |
自由度 |
変動 |
分散 |
観測された分散比 |
有意F |
| 回帰 |
6 |
84.8 |
14.13333 |
8 |
0.004904 |
| 残差 |
8 |
14.13333 |
1.766667 |
|
|
| 合計 |
14 |
98.93333 |
|
|
|
|
| |
係数 |
標準誤差 |
t |
P−値 |
下限 95% |
| 切片 |
86.53 |
0.907989 |
95.30216 |
1.64E-13 |
84.43951 |
| B社製 |
-3.00 |
0.840635 |
-3.56873 |
0.007307 |
-4.93851 |
| C社製 |
-4.60 |
0,840635 |
-5.47206 |
0.000593 |
-6.53851 |
| 10度 |
-3.33 |
1.085255 |
-3.07148 |
0.015314 |
-5.83594 |
| 20度 |
-1.67 |
1.085255 |
-1.53574 |
0.163153 |
-4.16927 |
| 30度 |
-0.33 |
1.085255 |
-0.30715 |
0.766574 |
-2.83594 |
| 40度 |
0.67 |
1.085255 |
0.614295 |
0.556083 |
-1.83594 |
(注)A社製、50度の列データを説明変数から削除しています。
図表42 要因を機械のみとした場合の回帰分析実行結果(一部)
概要
| 回帰統計 |
| 重相関R |
0.742 |
| 重決定R2 |
0.551 |
| 補正R2 |
0.476 |
| 標準誤差 |
1.924 |
| 観測数 |
15 |
| Ru= |
0.327 |
|
分散分析表
| |
自由度 |
変動 |
分散 |
観測された分散比 |
有意F |
| 回帰 |
2 |
54.53333 |
27.26667 |
7.369369 |
0.00817 |
| 残差 |
12 |
44.4 |
3.7 |
|
|
| 合計 |
14 |
98.93333 |
|
|
|
|
図表43 要因を温度のみとした場合回帰分析実行結果(一部)
概要
| 回帰統計 |
| 重相関R |
0.553 |
| 重決定R2 |
0.306 |
| 補正R2 |
0.028 |
| 標準誤差 |
2.620 |
| 観測数 |
15 |
| Ru= |
-0.388 |
|
分散分析表
| |
自由度 |
変動 |
分散 |
観測された分散比 |
有意F |
| 回帰 |
4 |
30.26667 |
7.566667 |
1.101942 |
0.407452 |
| 残差 |
10 |
68.66667 |
6.866667 |
|
|
| 合計 |
14 |
98.93333 |
|
|
|
|
図表41〜43についてRuを求めます。
図表44 Ru値一覧
| |
機械 |
温度 |
Ru |
| 1 |
○ |
○ |
0.607 |
| 2 |
○ |
− |
0.327 |
| 3 |
− |
○ |
-0.388 |
図表44より、Ruが最大のときは、(1)「機械、温度」の2要因を用いたときであることがわかります。
図表41より、生成量を表す回帰式は、
| |
|
|
|
-3.33(10度) |
| |
|
0.00(A社製) |
|
-1.67(20度) |
| 生成量=86.53 |
+ |
-3.00(B社製) |
+ |
-0.33(30度) |
| |
|
-4.60(C社製) |
|
0.67(40度) |
| |
|
|
|
0.00(50度) |
となります。上の式から機械はA社製、温度は40度のとき、生成量が最大になることがわかります。そのとき生成量は
生成量=86.53+0.00+0.67=87.20
と推定できます。
(注)A社製、50度の列データは削除したので、回帰係数は0とします。
●演習問題5
繰返しのある場合(各2回ずつ)の2要因実験データを解析しましょう。
次のようなデータを考えます。
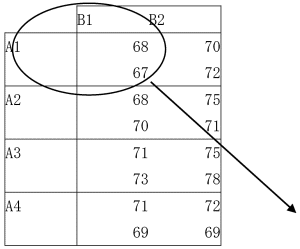
図表45
 |
A:温度 A1;10度
A2;20度
A3;30度
A4;40度
B:製法 B1;a
B2;b
|
表の見方:
A1B1、つまり10度で触媒がaのとき、2回実験をし、そのときの特性値は68と67でした。
|
問1 折れ線グラフを作りなさい。
問2 分散分析表を作りなさい。
問3 計画行列を作りなさい。
問4 回帰分析を実行しなさい。
|









