 |
【連載 統計解析力アップ講座】 演習；統計的品質管理(2)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
統計的品質管理講座の第２回です。統計的品質管理は、品質に影響をおよぼす異常原因を見つけ出して対処することが目的です。そして、この異常原因を見つけるための基礎となる考え方が検定という統計手法です。 ○例題１ 次のような変更前の収量に対して、製造条件の変更後の収量が、変更前と違いがあるかどうかを検定してください。
○検定とは 統計的品質管理では、まず異常原因になりそうな項目を要因として抽出し、その要因が変化したときに明らかな違いが発生したら異常原因だと判断します。検定とは、この明らかな違いがあるかどうかを統計的に判断する手法です。 違いがあるかどうかを比較する両者はいずれも正規分布であるとします。正規分布は平均値μと標準偏差σという２つのパラメータで数値化され、正規分布の面積が確率を表します。この正規分布の性質を利用することで、違いがあるかどうかを判断することができます。 具体的には、変更前の母集団の状態において変更後のデータの発生する確率が５％以下かどうかで判断します。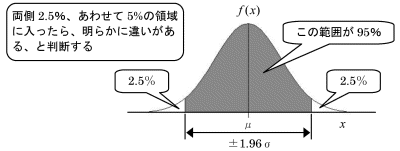 
正規分布ではデータの発生する確率が面積として表現されますが、95％の確率で発生する範囲は平均値μを挟んで±1.96σの範囲となることがわかっています。 つまり変更後の値が、変更前の分布の±1.96σの範囲に入らなかった場合、変更前と明らかに違いがあったと判断するのです。 ●例題１の答
まず、変更前の収量の正規分布を求めるとμ=100.1、σ=2.95と求められます。
変更後の収量の平均105が検定対象となりますが、この値はデータそのものでなく、データから計算して求めた値なので、上記の正規分布とそのまま比較できません。この正規分布から平均の正規分布を求める必要があります。 平均の正規分布の標準偏差σmは、データそのもののσより小さくなります。σmがどれぐらい小さくなるのかは、平均を求める元となったデータの個数nで決まります。平均値の標準偏差 σmは次の式で求められます。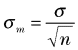 
この正規分布に対して、変更後の平均105がどれぐらいの確率で発生するのかを求め、その確率が５％未満であった時に変更前後で収量が明らかに異なっていると判断します。 すべての正規分布でμ±1.96σの発生確率が95％です。平均の正規分布についてこの範囲を求めると、 100.1−1.96×1.32＝97.51 〜 100.1＋1.96×1.32＝102.69
となります。変更後の平均105.0は、この97.51〜102.69の範囲より外側になるので、その発生確率は5%未満となることがわかります。したがって、変更後の収量は、変更前と比較して明らかに異なっていると判断できました。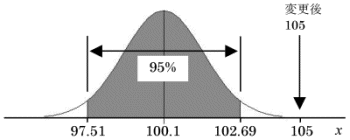 
○例題２ 次のように、変更前の収量のデータが少ないときの、製造条件を変更した後の収量のデータが変更前と違いがあるかどうかを検定してください。
●答
例題１のように変更前のデータが多い場合は、変更前の正規分布のデータの精度が高いので正規分布で検定を実施できます。しかしデータが少ないときは、正規分布では精度良く検定ができません。少ないデータで検定を実施する場合は正規分布ではない分布を使用します。このとき使用される分布はｔ分布と呼ばれるもので、正規分布と同様にその面積が確率を表す確率分布です。次の図のようにｔ分布の形は正規分布と良く似ていますが、若干山が低く裾野が広くなった形をしています。ｔ分布はデータの数にしたがってその分布の形が少しずつ異なります。データ数が大きくなるにつれ、その形は正規分布に近づいていき、データ数が無限大になったときｔ分布は正規分布と一致します。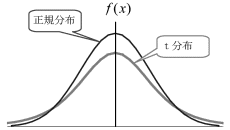 
このようなｔ分布を使用した検定をｔ検定と呼びます。ｔ検定ではデータからｔ値という値を計算し、正規分布のときと同様にｔ分布の中心を挟んだ、両側の面積が全体の95％となる領域にｔ値が入るか入らないかで検定します。 ｔ分布は中心値が０ですのでｔ値の絶対値を、ｔ分布の右側の2.5%を示す値と比較するだけで検定することができます。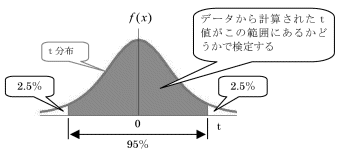 
ｔ値は次式で求められます。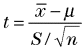 
ここで 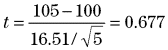 、Sは検定対象のデータの平均と標準偏差、μは比較元のデータの平均、ｎはデータ数です。データからｔ値を求めると次のようになります。
ｔ分布の右側の2.5%を示す値は、ExcelのTINV関数で次のように求められます。ここで0.05は確率の５%、５はデータ数です。 TINV (0.05, 5-1) = 2.776
求めたｔ値（の絶対値）がTINVの値より小さくなったので、変更後の収量は変更前と違いがあるとはいえない、という結果になりました。 ○例題３ 例題２と同じデータで、標準偏差について検定してください。
●答
平均値と同じ考え方で、標準偏差についても検定を実施することができます。ただし、標準偏差は正規分布で検定することができません。ばらつきが正規分布にならないのです。標準偏差を２乗した数を分散といいます。分散は、比を取るとF分布という分布になります。標準偏差の検定にはこの性質を利用します。比較したいデータ各々の標準偏差を２乗し、その比をとってF分布上で検定します。この分散の比のことをF値または分散比といいます。 F分布は次の図のような形の分布で、面積が確率を表す確率分布です。計算したF値（分散比）がF分布上の95%の範囲に入るか入らないかで、標準偏差について検定することができます。F分布を使用することからこの検定をF検定と呼びます。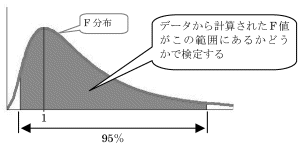 
図2-16
F検定は、標準偏差の２乗の比を計算しF分布の95%の値を求めれば実施できます。Excelの「分析ツール」にはF検定を実施するツールが含まれていますので、ここでは「分析ツール」によるF検定の実施結果を次に示します。 
「観測された分散比」と示された値がF値です。この値を「F境界値両側」で示された値と比較することで標準偏差についての検定を実施しますが、F値が１より大きいか小さいかで判定の仕方が次のように異なります。 F値が１より小さい場合は、「F境界値 両側」の値よりF値が小さいときに違いがあると判断します。 F値が１より大きい場合は、「F境界値 両側」の値よりF値が大きいときに違いがあると判断します。 今回の結果では、F値が１より小さい0.0459で「F境界値両側」の値0.1565より小さくなっているので、変更後の収量の標準偏差が変更前と明らかに異なっていると判断できます。 お疲れ様でした。第３回では分散分析について解説します。 ＜参考文献＞ ・「Excelでできる統計的品質管理」（同友館） ・「Excelで学ぶ営業・企画・マーケティングのための実験計画法」（オーム社） ・「新編 統計的方法」（日本規格協会)
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||