





|
【連載 統計解析力アップ講座】 演習;実験計画法とタグチメソッド(8)
|
空欄を埋めながらタグチメソッドを学びましょう。 □タグチメソッドとは 工学手法 タグチメソッドとは(1)が創始した世界でも類のない(2)です。日本では(3)ともよばれています。 タグチメソッドは(4)段階で適用されるべき手法です。 コストを抑えて(5)の少ないものを開発する手法です。従来の手法は(6)にあわせようとします。この点は大きく違うところです。 実験計画法と比較 タグチメソッドと実験計画法の違いは何でしょう? 実験計画法は(7)です。タグチメソッドは(2)です。実験計画法は(8)の発見・自然の法則の発見です。これに較べて、タグチメソッドは自然の法則にさからって(9)にないものを作りだすのです。だから(2)です。 因子について考えます。実験計画法になくて、タグチメソッドにでてくる因子が(10)です。 筆者は環境因子ともよんでいます。タグチメソッドは(11)が利用者の立場で、たとえば振動のあるところ、高温多湿のところなど、悪条件を積極的に作り実験します。このようなことは実験計画法では通常考慮しません。 悪条件下で製品が使用され、トラブルが発生するのは、製品に(5)が多いからだとタグチメソッドはいいます。この(5)を設計時に押さえ込むのです。 □タグチメソッドの特徴 2段階設計(ロバストデザイン) 実験計画法は目標値を実現しようと効いている制御因子とその水準を探します。タグチメソッドはまず、(5)を抑えます。そして目標値に近づけるのです。これを2段階設計とか米国ではロバストデザイン(robust design)と呼んでいます。 SN比 SN比は通信工学のアナロジーです。SはSignal、NはNoiseです。Sは信号なので、大きいほどよく、Nはノイズなので小さいほどいいのです。SとNの比 S/Nを考えます。数学的に取り扱いやすくするために、常用対数LOGをとり、さらに10倍します。したがって式にすると、 SN比=(12)です。 SN比が大きいほどばらつきが少ないのです。ばらつきがすくないということは(13)いるということです。 直交表 実験計画法でもタグチメソッドでも直交表を使用して実験の(14)割付(実験計画のこと)をします。 タグチメソッドで用いる直交表はL12、L18、L36です。 L12直交表 画像をクリックすると拡大画像が表示されます。 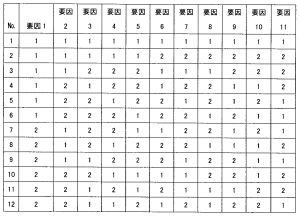
L18直交表 画像をクリックすると拡大画像が表示されます。 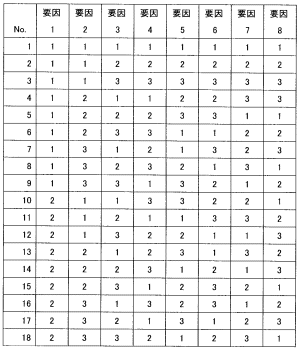
L36直交表 画像をクリックすると拡大画像が表示されます。 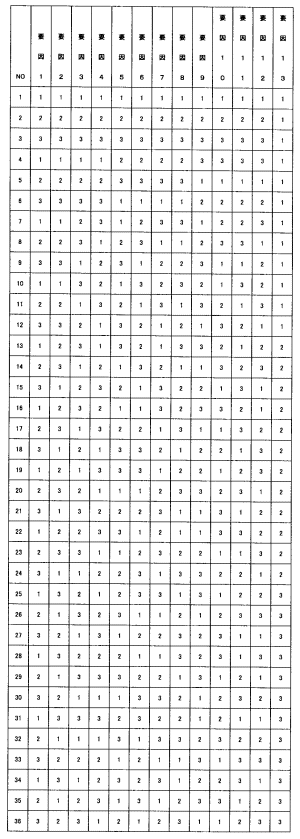
3つの直交表のうち一番使用されているのは(15)のようです。なぜでしょうか? 実験回数が18回の割には、扱える制御因子が8個と多いからです。しかも1つだけ2水準で残りは3水準が7つもあります。 通常の実験計画法の直交表は2水準系(L4,L8,L16,L32、L64)、3水準系(L9、 L27、L81)です。 これらの直交表は交互作用項があるかどうかを調べることができます。 タグチメソッドの直交表は交互作用項を調べることはできません。交互作用があるような制御因子は不安定で市場に出たとき、再現性がないと考えているからです。 基本機能 課題;不良率をいかに低減するか を考えます。 ある会社で不良率が高くて困っています。 不良率を低減するにはどうすればよいのでしょうか。不良率を特性値yに、yの増減に影響がありそうな要因を説明変数として、回帰分析法がよく適用されます。 成功するケースもありますが、もぐらたたきだといわれています。 根本から改善しなければ、また別の問題が発生します。 だからもぐらたたきだといわれます。 因果分析的なことをやってはならないといわれています。 タグチメソッドの出番です。 タグチメソッドでは(16)を考えます。 たとえば、複写機の紙送り機構の改善を考えます。 キーワードは基本機能です。基本機能は(17)の基本概念です。(17)とは、車のアクセルとスピードの関係のように、入力の変化に対応して出力が変化する特性のことです。 (17)の例については、演習問題を参照してください。 基本機能はたとえば「紙を10枚入れたら、10秒でコピーが出てくる」。 このように、線形になるように制御因子と水準を見つけるのです。 誤差因子も考慮します。誤差因子とは環境因子のことでした。 湿気が多いとき、少し振動しているとき、つまり悪環境のときでも基本機能を実現するように設計するのです。 機能が安定していること、つまりばらつきが少ないときほど、SN比は(18)くなります。 動特性のSN比は以下のようです。 SN比=10*LOG(β²/σ²)ここで、 β;傾き σ²;誤差の分散 LOG;常用対数 基本機能こそタグチメソッドの最大の特徴と言っても過言ではないでしょう。 解答 (1)田口玄一博士、(2)工学手法、(3)品質工学、(4)開発・設計、 (5)ばらつき、(6)目標値、(7)科学、(8)事実、(9)自然界、(10)誤差因子、 (11)開発者(設計者)、(12)10LOG(S/N)、(13)安定して、(14)割付、 (15)L18直交表、(16)基本機能、(17)動特性、(18)大き □演習問題 砂時計の事例のように入力信号M(砂の量)と特性値y(時間)の関係が下の図のように原点を通る比例式になるような入力と出力を見つけることが動特性では重要です。 このような事例を挙げなさい。 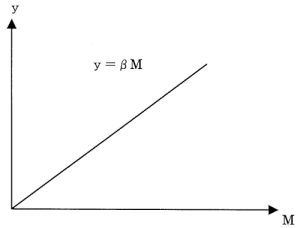
◆射出成形における金型の寸法(入力)と製品寸法(出力) ◆荷重(入力)と摩擦力(出力) ◆ばねの力(入力)と変位(出力) ◆イースト菌の発酵時間(入力)と発酵力の平方根(出力) ◆電着塗装(入力)と膜圧(出力) ◆自動原稿送り装置のセットする紙の枚数(入力)と総給紙時間(出力) ◆鋼の熱処理の焼戻し温度(入力)と硬さ(出力) ◆回転式流量計の流量(入力)と回転子の回転数(出力) ◆複写機の原画の線幅(μ)(入力)とコピーの線幅(出力) ◆クロレラの培養時間(入力)とクロレラの数の対数(出力) ◆MOSトランジスタのゲート電圧(入力)とドレイン電流の対数(出力) ◆プリンタの紙送り機構の距離(入力)と回転角(出力) ◆カップ式自動販売機のコーヒー粉量(入力)とコーヒー濃度(出力) ◆鋳造の荷重(入力)と変形量(出力) 参考文献 「品質工学」誌、品質工学会 広瀬健一・上田太一郎編著 「Excelでできるタグチメソッド解析法入門」同友館 宮川雅巳「品質を獲得する技術」日科技連 |


