| |
 |
【連載 統計解析力アップ講座】
演習:統計的品質管理(5)
| |
 |
統計的品質管理講座の第5回です。今回は、複数の原因と結果の関係を数式化してデータの予測を可能とする分析手法−重回帰分析・数量化理論I類−についての演習です。
○例題1
ある原料から精製される製品の製造条件と収量のデータがあります。投入速度、反応炉温度、反応炉圧力が収量に対してどのように影響しているか分析してください。
| No. |
投入速度 |
反応炉温度 |
反応炉圧力 |
収量 |
| 1 |
5.20 |
241.8 |
2.08 |
78.8 |
| 2 |
5.59 |
240.5 |
2.08 |
65.3 |
| 3 |
5.47 |
237.1 |
2.00 |
77.2 |
| 4 |
5.42 |
244.1 |
2.13 |
66.1 |
| 5 |
5.42 |
249.4 |
2.06 |
75.6 |
| 6 |
5.36 |
253.7 |
2.03 |
83.8 |
| 7 |
5.29 |
253.4 |
2.04 |
86.7 |
| 8 |
5.30 |
250.0 |
2.15 |
69.1 |
| 9 |
5.05 |
255.2 |
1.98 |
90.7 |
| 10 |
5.18 |
255.2 |
1.99 |
92.1 |
| 11 |
5.25 |
259.0 |
2.07 |
93.9 |
| 12 |
5.18 |
246.7 |
2.01 |
87.6 |
| 13 |
5.18 |
249.6 |
2.11 |
74.9 |
| 14 |
5.09 |
253.5 |
2.13 |
83.2 |
| 15 |
5.07 |
234.0 |
2.14 |
78.9 |
| 16 |
5.88 |
243.2 |
2.08 |
67.7 |
| 17 |
5.55 |
250.3 |
2.13 |
67.2 |
| 18 |
5.56 |
243.2 |
2.12 |
62.7 |
| 19 |
5.50 |
245.8 |
2.15 |
70.1 |
| 20 |
5.58 |
243.3 |
2.11 |
66.6 |
●答
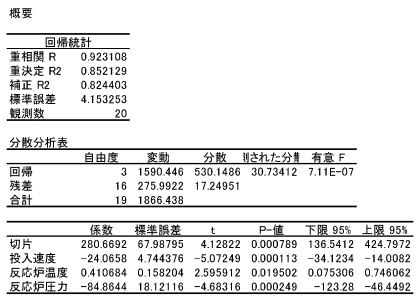
重回帰分析を実施することによって、このデータから原料の投入速度、反応炉の温度および圧力という要因が、収量に対してどのように影響しているのかを分析することができます。Excel分析ツールの[回帰分析]を実行すると次のような結果が表示されます。
図4-5左下の部分に「係数」で示されている数値を使用して、収量を表す回帰式が求められます。
| 収量=280.6692 |
−24.0658 |
×(投入速度) |
| +0.410684 |
×(反応炉温度) |
| −84.8644 |
×(反応炉圧力) |
この回帰式を重回帰分析による回帰式という意味で重回帰式と呼ぶこともあります。この式から、収量を上げるには投入速度を低く、反応炉温度を高く、反応炉圧力を低くすればよいことがわかります。
要因の影響の大きさはt、P-値で比較することができます。たとえばt値の絶対値の大きい「投入速度」「反応炉圧力」「反応炉温度」の順で結果に対する影響が大きいことがわかります。P-値では値の小さいものほど影響が大きい要因であることを示します。
また、tまたはP-値によって各要因が結果に対して本当に影響しているかどうかを判定できます。tの絶対値が√2以上であるか、P-値の値が20%以下なら、影響があると判定します。今回の結果ではすべての要因が結果に対して影響があるといえます。もし影響していないと判定された要因があった場合、その要因を除外して[回帰分析]を実施した結果から求めた回帰式が最適な回帰式となります。
重回帰式を利用すると要因が変化したときの収量を予測することができます。たとえば収量を上げるために投入速度を5.0、反応炉温度を260.0、反応炉圧力を2.00としたときの収量は、280.6692−24.0658×5.0+0.410684×260.0−84.8644×2.00= 97.39になると予測できます。
○例題2
次のデータについて、分析してください。
| No. |
原料メーカー |
投入速度 |
反応炉圧力 |
反応炉温度 |
添加剤 |
冷却速度 |
収量 |
| 1 |
A |
5.95 |
2.03 |
245.4 |
X |
14.3 |
50.3 |
| 2 |
A |
5.72 |
2.02 |
234.5 |
X |
15.7 |
56.7 |
| 3 |
A |
5.39 |
2.10 |
250.1 |
X |
9.8 |
58.0 |
| 4 |
A |
5.53 |
2.04 |
245.4 |
X |
15.4 |
62.3 |
| 5 |
A |
5.45 |
1.96 |
242.9 |
X |
14.0 |
67.0 |
| 6 |
A |
5.23 |
2.05 |
257.6 |
Y |
12.7 |
68.2 |
| 7 |
A |
5.43 |
2.10 |
257.5 |
X |
5.3 |
67.5 |
| 8 |
A |
5.51 |
1.99 |
243.6 |
X |
12.9 |
68.0 |
| 9 |
A |
5.49 |
2.00 |
248.0 |
X |
16.9 |
69.3 |
| 10 |
A |
5.60 |
1.97 |
249.7 |
X |
7.6 |
68.5 |
| 11 |
B |
5.53 |
2.13 |
247.0 |
X |
4.5 |
62.0 |
| 12 |
B |
5.32 |
2.09 |
243.5 |
X |
2.0 |
65.8 |
| 13 |
B |
5.25 |
2.06 |
254.0 |
X |
3.8 |
73.6 |
| 14 |
B |
5.82 |
2.15 |
270.4 |
Y |
3.2 |
76.4 |
| 15 |
B |
5.36 |
2.11 |
252.9 |
X |
5.0 |
77.5 |
| 16 |
B |
5.58 |
1.97 |
252.4 |
X |
10.0 |
78.0 |
| 17 |
C |
5.60 |
2.03 |
247.8 |
Y |
18.4 |
69.2 |
| 18 |
C |
5.46 |
2.01 |
250.8 |
X |
4.2 |
77.2 |
| 19 |
C |
5.06 |
1.97 |
255.1 |
X |
15.3 |
82.2 |
| 20 |
C |
5.45 |
2.02 |
257.6 |
X |
10.1 |
81.9 |
●答
原料メーカーと添加剤が数値でないため、[回帰分析]が実行できません。そこで、次のように数値化した表に変換します(数値でない要因について任意の1列を削除していることに注意ください。ここでは原料メーカCと添加剤Yの項目を削除しています)。
| No. |
原料メーカー
A |
原料メーカー
B |
投入速度 |
反応炉圧力 |
反応炉温度 |
添加剤
X |
冷却
速度 |
収量 |
| 1 |
1 |
0 |
5.95 |
2.03 |
245.4 |
1 |
14.3 |
50.3 |
| 2 |
1 |
0 |
5.72 |
2.02 |
234.5 |
1 |
15.7 |
56.7 |
| 3 |
1 |
0 |
5.39 |
2.10 |
250.1 |
1 |
9.8 |
58.0 |
| 4 |
1 |
0 |
5.53 |
2.04 |
245.4 |
1 |
15.4 |
62.3 |
| 5 |
1 |
0 |
5.45 |
1.96 |
242.9 |
1 |
14.0 |
67.0 |
| 6 |
1 |
0 |
5.23 |
2.05 |
257.6 |
0 |
12.7 |
68.2 |
| 7 |
1 |
0 |
5.43 |
2.10 |
257.5 |
1 |
5.3 |
67.5 |
| 8 |
1 |
0 |
5.51 |
1.99 |
243.6 |
1 |
12.9 |
68.0 |
| 9 |
1 |
0 |
5.49 |
2.00 |
248.0 |
1 |
16.9 |
69.3 |
| 10 |
1 |
0 |
5.60 |
1.97 |
249.7 |
1 |
7.6 |
68.5 |
| 11 |
0 |
1 |
5.53 |
2.13 |
247.0 |
1 |
4.5 |
62.0 |
| 12 |
0 |
1 |
5.32 |
2.09 |
243.5 |
1 |
2.0 |
65.8 |
| 13 |
0 |
1 |
5.25 |
2.06 |
254.0 |
1 |
3.8 |
73.6 |
| 14 |
0 |
1 |
5.82 |
2.15 |
270.4 |
0 |
3.2 |
76.4 |
| 15 |
0 |
1 |
5.36 |
2.11 |
252.9 |
1 |
5.0 |
77.5 |
| 16 |
0 |
1 |
5.58 |
1.97 |
252.4 |
1 |
10.0 |
78.0 |
| 17 |
0 |
0 |
5.60 |
2.03 |
247.8 |
0 |
18.4 |
69.2 |
| 18 |
0 |
0 |
5.46 |
2.01 |
250.8 |
1 |
4.2 |
77.2 |
| 19 |
0 |
0 |
5.06 |
1.97 |
255.1 |
1 |
15.3 |
82.2 |
| 20 |
0 |
0 |
5.45 |
2.02 |
257.6 |
1 |
10.1 |
81.9 |
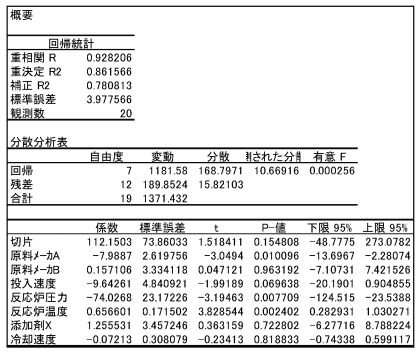
この表について[回帰分析]を実行すると次のような結果が得られます。
どの要因が収量に対して本当に影響しているかを見るにはtの値を利用しますが、数値が2行にわたっている要因は「tのレンジ」を求めます。たとえば原料メーカーについてはtの最大値であるメーカBの0.047121から最小値であるメーカAの−3.0494を引いて3.096521と求められます。
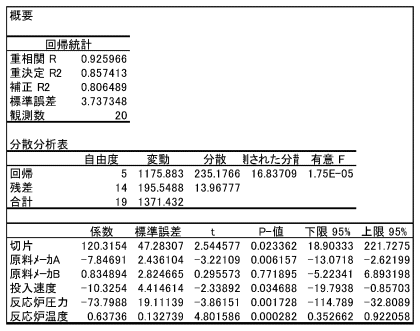
tの絶対値またはtのレンジが√2=1.414以上となる「原料メーカー」「投入速度」「反応炉圧力」「反応炉温度」が収量に対して本当に影響のある要因と判定できます。最適な回帰式は影響のある要因だけを対象として[回帰分析]を実行した結果から次のように求められます。
このように要因を数値化して実施する重回帰分析を数量化理論I類と呼びます。
○例題3
次のデータについて、回帰分析を利用して分析してください。
| |
材料 |
| 加工温度 |
A |
B |
C |
D |
| 110 |
4.46 |
4.66 |
4.95 |
5.06 |
| 125 |
4.48 |
4.78 |
5.01 |
5.21 |
| 140 |
4.63 |
4.98 |
5.05 |
5.23 |
●答
この例題は第3回の例題2です。次のような表を作成すると[回帰分析]を利用して分散分析を実施することができます(要因について任意の1列を削除していることに注意ください。ここでは加工温度140と材料Dの列を削除しています)。
| 加工温度 |
材料 |
|
| 110 |
125 |
A |
B |
C |
製品特性 |
| 1 |
0 |
1 |
0 |
0 |
4.46 |
| 0 |
1 |
1 |
0 |
0 |
4.48 |
| 0 |
0 |
1 |
0 |
0 |
4.63 |
| 1 |
0 |
0 |
1 |
0 |
4.66 |
| 0 |
1 |
0 |
1 |
0 |
4.78 |
| 0 |
0 |
0 |
1 |
0 |
4.98 |
| 1 |
0 |
0 |
0 |
1 |
4.95 |
| 0 |
1 |
0 |
0 |
1 |
5.01 |
| 0 |
0 |
0 |
0 |
1 |
5.05 |
| 1 |
0 |
0 |
0 |
0 |
5.06 |
| 0 |
1 |
0 |
0 |
0 |
5.21 |
| 0 |
0 |
0 |
0 |
0 |
5.23 |
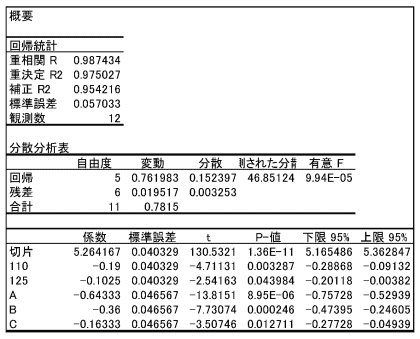
[回帰分析]を実行すると次のような結果が得られます。
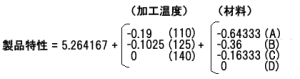
tのレンジを求める際、表示されていない項目の係数が0であることに注意ください。たとえば加工温度では140の係数が0で、材料ではDの係数が0になります。したがってtのレンジを求めると加工温度では0−(−4.71131)=4.71131、材料では0−(−3.50746)=3.50746となります。
どちらのtのレンジも√2=1.414以上となり、製品特性に対して本当に影響している要因といえます。これより、最適な回帰式は次のように求められます。
[回帰分析]を利用すると分散分析だけでなく、実験計画法も簡単に解析することができます。第6回は効率的な実験を行う実験計画法についての演習です。
<参考文献>
・「Excelでできる統計的品質管理入門」(同友館)
・「Excelで学ぶ回帰分析入門」(オーム社)
著者紹介
近藤 宏(こんどう ひろし)
三菱電機(株)勤務。業務用空調機の開発、品質、生産管理業務に携わりながら統計的品質管理(SQC)・タグチメソッドを学ぶ。最近は統計解析手法、データマイニング手法を技術系だけでなく事務系範囲をも対象とした手法の啓蒙に着手している。主著に「Excelでできるデータ解析入門」「Excelでできる統計的品質管理入門」(以上同友館)、共著に「Excelで学ぶ営業企画マーケティングのための実験計画法」「Excelで学ぶ時系列分析と予測」(以上オーム社)、「Excelでできるタグチメソッド解析法入門」(同友館)がある。
|

|
|