| |
 |
【連載 統計解析力アップ講座】
演習:統計的品質管理(6)
| |
 |
いよいよ統計的品質管理講座の最終回です。
最終回は実験を効率的に実施する手法−実験計画法−についての演習です。
○例題1
ある製品の製造に関して「材料」「加工温度」「加工時間」によって製品の特性に違いがあるかどうかを確かめるため実験を行うこととして、現在までに次のようなデータが取得されています。このデータについて分析してください。
| |
加工温度 |
100℃ |
125℃ |
| |
加工時間 |
5分 |
10分 |
5分 |
10分 |
| 材料 |
A |
5.1 |
未測定 |
未測定 |
6.0 |
| B |
未測定 |
8.2 |
9.5 |
未測定 |
●答
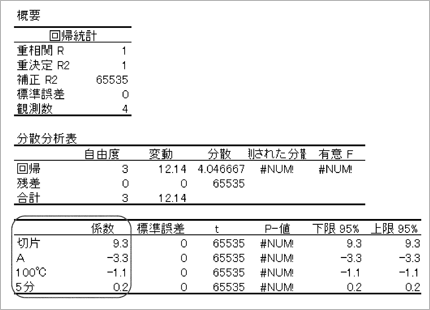
未測定のデータがあり、この状態では[分散分析]で分析することができません。[回帰分析]なら分析できるかもしれませんので、この結果を次のような回帰分析を実行できる表に書き換えます。
| No |
A |
100℃ |
5分 |
特性 |
| 1 |
1 |
1 |
1 |
5.1 |
| 2 |
1 |
0 |
0 |
6.0 |
| 3 |
0 |
1 |
0 |
8.2 |
| 4 |
0 |
0 |
1 |
9.5 |
この表についてExcelの[回帰分析]を実行すると次のような結果が得られます。
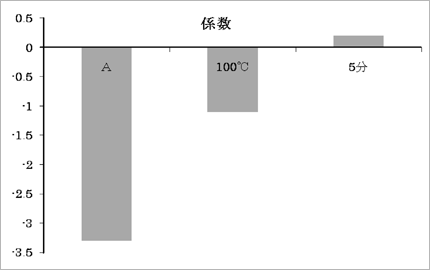
t やP-値はうまく算出されませんが、各要因の係数は求められています。この係数を並べて折れ線グラフで示すと、次のように要因の影響の大きさを比べることができます。
データが少なくても、要因の影響の大きさを比較することができました。つまり、要因を分析するために必要なデータ数は、例題に示した表を埋めるほど多くないのです。
要因の分析に必要な、最低限のデータ数は直交表で示されます。実は、前述の回帰分析を実行するために作成した表が、L4直交表(L4直交表とも)といわれる直交表になっています。
| No |
A |
100℃ |
5分 |
| 1 |
1 |
1 |
1 |
| 2 |
1 |
0 |
0 |
| 3 |
0 |
1 |
0 |
| 4 |
0 |
0 |
1 |
直交表は要因の項目の出現回数が、バランス良く最低限の回数となって現れる表です。たとえば表に示された4回の実験で、材料がAの回数、Bの回数、加工温度が100℃の回数、125℃の回数、加工時間が5分の回数、10分の回数ともすべて2回ずつになっていることがわかります。
直交表にはこの他に、次のようなL8直交表、L9直交表、L18直交表などがあり、要因の数に合わせて直交表を選ぶことができます。このように直交表を利用することで実験回数を節約し、実験を効率的に実施する手法を実験計画法と呼びます。
L8直交表
| No. |
A |
B |
C |
D |
E |
F |
G |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
| 3 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
| 4 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
| 5 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
| 6 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
| 7 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
| 8 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
L9直交表
| No. |
A |
B |
C |
D |
| 1 |
1 |
1 |
1 |
1 |
| 2 |
1 |
2 |
2 |
2 |
| 3 |
1 |
3 |
3 |
3 |
| 4 |
2 |
1 |
2 |
3 |
| 5 |
2 |
2 |
3 |
1 |
| 6 |
2 |
3 |
1 |
2 |
| 7 |
3 |
1 |
3 |
2 |
| 8 |
3 |
2 |
1 |
3 |
| 9 |
3 |
3 |
2 |
1 |
L18直交表
| No. |
A |
B |
C |
D |
E |
F |
G |
H |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
| 3 |
1 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
| 4 |
1 |
2 |
1 |
1 |
2 |
2 |
3 |
3 |
| 5 |
1 |
2 |
2 |
2 |
3 |
3 |
1 |
1 |
| 6 |
1 |
2 |
3 |
3 |
1 |
1 |
2 |
2 |
| 7 |
1 |
3 |
1 |
2 |
1 |
3 |
2 |
3 |
| 8 |
1 |
3 |
2 |
3 |
2 |
1 |
3 |
1 |
| 9 |
1 |
3 |
3 |
1 |
3 |
2 |
1 |
2 |
| 10 |
2 |
1 |
1 |
3 |
3 |
2 |
2 |
1 |
| 11 |
2 |
1 |
2 |
1 |
1 |
3 |
3 |
2 |
| 12 |
2 |
1 |
3 |
2 |
2 |
1 |
1 |
3 |
| 13 |
2 |
2 |
1 |
2 |
3 |
1 |
3 |
2 |
| 14 |
2 |
2 |
2 |
3 |
1 |
2 |
1 |
3 |
| 15 |
2 |
2 |
3 |
1 |
2 |
3 |
2 |
1 |
| 16 |
2 |
3 |
1 |
3 |
2 |
3 |
1 |
2 |
| 17 |
2 |
3 |
2 |
1 |
3 |
1 |
2 |
3 |
| 18 |
2 |
3 |
3 |
2 |
1 |
2 |
3 |
1 |
○例題2
焼結金属材料の製造工程でケイ素不純物量を低減するため、次のような要因と項目をあげて実験することとしました。
| 要因 |
項目1 |
項目2 |
| 素材混合時間 |
30分 |
60分 |
| 潤滑材添加率 |
1.20% |
2.50% |
| 金属添加率 |
0.10% |
0.20% |
| 成形圧力 |
300MPa |
500MPa |
| 焼結温度 |
1000℃ |
1200℃ |
| 再圧縮圧力 |
50MPa |
70MPa |
すべて2項目の要因が6つですので、L8直交表による実験計画法が適用できます。次のようにL8直交表のA〜F列に要因を割り付けます。余ったG列は使用しないことになります。
| No |
素材混
合時間 |
潤滑材
添加率 |
金 属
添加率 |
成形圧力 |
焼結温度 |
再圧縮
圧 力 |
G
(余) |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
| 3 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
| 4 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
| 5 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
| 6 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
| 7 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
| 8 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
No.1〜8について各要因の項目どおりに条件を設定し、8回の実験を実施した結果、次のようなデータが得られました。このデータについて分析してください。
| No |
素材混
合時間 |
潤滑材
添加率 |
金 属
添加率 |
成形圧力 |
焼結温度 |
再圧縮
圧 力 |
G
(余) |
| 1 |
30分 |
1.20% |
0.10% |
300MPa |
1000℃ |
50MPa |
0.86 |
| 2 |
30分 |
1.20% |
0.10% |
500MPa |
1200℃ |
70MPa |
1.19 |
| 3 |
30分 |
2.50% |
0.20% |
300MPa |
1000℃ |
70MPa |
0.70 |
| 4 |
30分 |
2.50% |
0.20% |
500MPa |
1200℃ |
50MPa |
1.08 |
| 5 |
60分 |
1.20% |
0.20% |
300MPa |
1200℃ |
50MPa |
1.13 |
| 6 |
60分 |
1.20% |
0.20% |
500MPa |
1000℃ |
70MPa |
1.30 |
| 7 |
60分 |
2.50% |
0.10% |
300MPa |
1200℃ |
70MPa |
0.97 |
| 8 |
60分 |
2.50% |
0.10% |
500MPa |
1000℃ |
50MPa |
1.30 |
●答
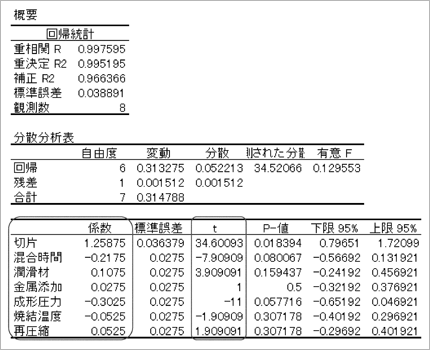
実験計画法の解析は前回の数量化理論I類と同じです。実験結果を次のような回帰分析を実行できる表に変更して、Excelの[回帰分析]を実行します。
| No |
混合時間
30分 |
潤滑材
1.20% |
金属添加
0.10% |
成形圧力
300MPa |
焼結温度
1000℃ |
再圧縮
50MPa |
ケイ素
含有率% |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.86 |
| 2 |
1 |
1 |
1 |
0 |
0 |
0 |
1.19 |
| 3 |
1 |
0 |
0 |
1 |
1 |
0 |
0.70 |
| 4 |
1 |
0 |
0 |
0 |
0 |
1 |
1.08 |
| 5 |
0 |
1 |
0 |
1 |
0 |
1 |
1.13 |
| 6 |
0 |
1 |
0 |
0 |
1 |
0 |
1.30 |
| 7 |
0 |
0 |
1 |
1 |
0 |
0 |
0.97 |
| 8 |
0 |
0 |
1 |
0 |
1 |
1 |
1.30 |
次のような回帰分析結果が得られます。
t の絶対値が√2=1.414以上となった要因:素材混合時間、潤滑材添加率、成形圧力、焼結温度、再圧縮圧力がケイ素含有率に影響がある要因だと判断できます。
不純物であるケイ素含有率を下げるには、要因の係数が小さいほうの項目を選べばよいので、素材混合時間30分、潤滑材添加率2.5%、成形圧力300MPa、焼結温度1000℃、再圧縮圧力70MPaとすればよいことがわかります。
また、その時のケイ素含有率は、1.25875−0.2175−0.3025−0.0525=0.686%になると予測できます。
例題1では表示されなかったt、P-値などの値がこの結果では表示されています。これは、直交表に要因を割りつけなかった列(G列)があったためです。直交表の列に余裕がある場合はこのように回帰分析結果にt、P-値が表示され、精度良い判定をすることができます。
以上のように実験計画法を利用すると、効率的な実験によって要因の効果を分析することができます。ただし、実験計画法には要因の性質によって注意しなければならない点や、異なる手順によって解析結果を評価する方法があります。本講座では詳しく解説できませんでしたが、実務に適用する場合は実験計画法の書籍、文献を参照いただきたいと思います。
また、実験計画法の解析手順はそのままタグチメソッドの解析に適用できます。実はL18直交表はタグチメソッド用の直交表です。本講座の演習内容を基本としてタグチメソッドにもぜひ挑戦していただきたいと思います。
これで統計的品質管理の演習を終わります。本講座の内容が皆様のお役に立つことを願っております。ありがとうございました。
<参考文献>
・「Excelでできる統計的品質管理入門」(同友館)
・「Excelでできるタグチメソッド解析法入門」(同友館)
著者紹介
近藤 宏(こんどう ひろし)
三菱電機(株)勤務。業務用空調機の開発、品質、生産管理業務に携わりながら統計的品質管理(SQC)・タグチメソッドを学ぶ。最近は統計解析手法、データマイニング手法を技術系だけでなく事務系範囲をも対象とした手法の啓蒙に着手している。主著に「Excelでできるデータ解析入門」「Excelでできる統計的品質管理入門」(以上同友館)、共著に「Excelで学ぶ営業企画マーケティングのための実験計画法」「Excelで学ぶ時系列分析と予測」(以上オーム社)、「Excelでできるタグチメソッド解析法入門」(同友館)がある。
|

|
|