|
|
|
|
1 |
統計の基礎 |
|
|
|
|
|
本マニュアルは、タグチメソッドデータの解析に回帰分析法を用いて |
|
|
行う立場をとる。したがって、本章では回帰分析に関連する統計手法 |
|
|
(相関と回帰、重回帰分析、実験計画法)について解説する。 |
|
|
|
|
|
|
|
1.1. |
相関と回帰 |
|
|
|
|
1.1.1. |
相関とは |
|
|
|
|
|
相関とはある量とある量との線形な関係度(関連度)を表す指標で |
|
|
ある。式で示すと、データxi,yi(i=1,2,…,n)が与え |
|
|
られたとき、xとyの相関係数rは |
|
|
|
|
|
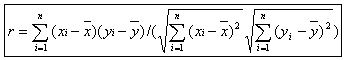
|
|
|
|
|
|
となる。ここで、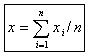 (xの平均), (xの平均),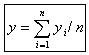 (yの平均) (yの平均) |
|
|
である。rは−1と1の間の値をとり、1(あるいは−1)に近いとき、 |
|
|
強い相関(関連)があり、0に近いとき相関(関連)がないという。 |
|
|
+の値のときは正の相関があり、ある量xが増加すると、ある量yも |
|
|
増加する。相関があり、ある量xが増加すると、ある量yが減少する。 |
|
|
|
|
|
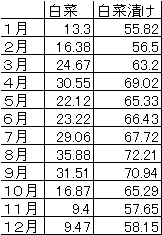
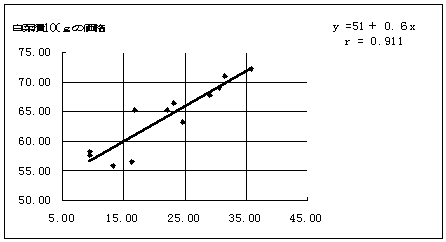
実際の例で説明する。表1のデータは毎月の白菜100gの価格と |
|
|
白菜漬100gの価格である。図1は横軸(x軸)に白菜の価格、 |
|
|
縦軸(y軸)に白菜漬の価格をとった散布図である。白菜の価格が |
|
|
上がると白菜漬の価格も上がることがわかる。相関係数は0.911なので |
|
|
比較的強い正の相関があることになる。 |
|
|
|
|
|
表1 白菜100gと白菜漬100gの価格(円) |
|
|
|
|
|
「食品商業」95年1月号 |
|
|
|
|
|
|
|
|
図1 価格の関係 |
|
|
|
|
|
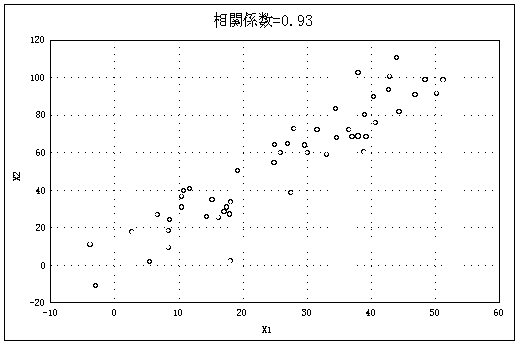
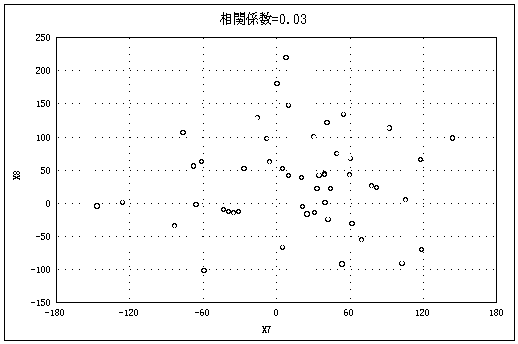
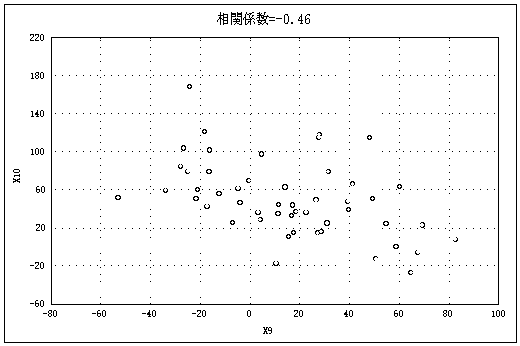
図2はいろいろなケースの散布図とそのときの相関係数である |
|
|
(データ数=50)。 |
|
|
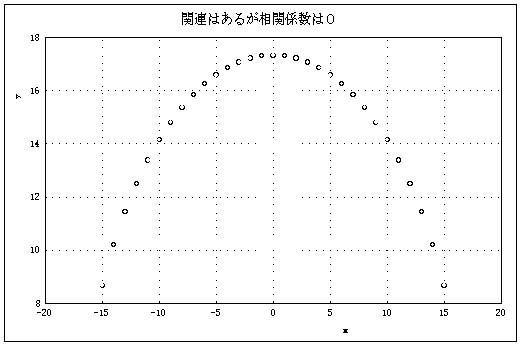
また、図3はxとyとは何らかの関係はあるが相関係数は0となっている。 |
|
|
相関係数はあくまで線形の関係を示すモノサシであることに注意のこと。 |
|
|
|
|
|
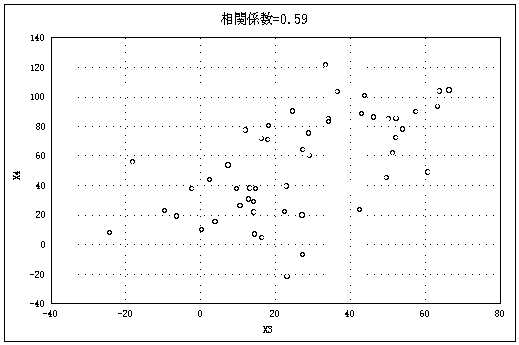
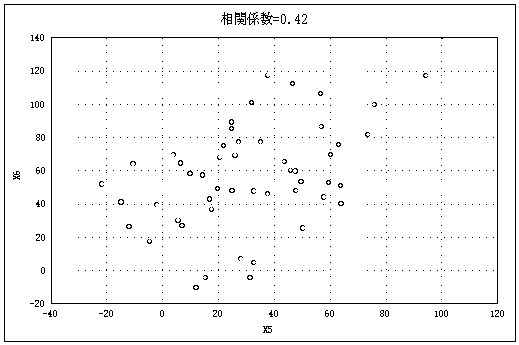
図2 いろいろな散布図と相関係数(n=50)(以下5点、図2―(1)〜(5)) |
|
|
|
|
|
|
|
|
図2―(1) |
|
|
|
|
|
|
|
|
図2―(2) |
|
|
|
|
|
|
|
|
図2―(3) |
|
|
|
|
|
|
|
|
図2―(4) |
|
|
|
|
|
|
|
|
図2―(5) |
|
|
|
|
|
|
|
|
図3 相関係数が0となる例 |
|
|
|
|
|
相関の有無の判定は、通常t検定を用いるが、本書では筆者の提案 |
|
|
する簡便法を紹介する。(上田“相関を見つける簡便法” |
|
|
「オペレーションズ・リサーチ」1997年7月号) |
|
|
|
|
|
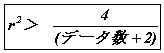
|
|
|
|
|
|
が成立するとき相関があると判定する。 |
|
|
白菜の例ではr=0.911の自乗は0.830で、4/14=0.290より大きいので |
|
|
相関があると判定する。 |
|
|
|
|
1.1.2. |
単回帰式(回帰直線) |
|
|
|
|
|
データの組xiとyiがあり、xでyを説明する式、y=a+bxを単回帰式 |
|
|
(あるいは回帰直線)という。単とは説明する変数xが1個である |
|
|
からである(複数個のときを重回帰式という)。a(y切片)とb(傾き) |
|
|
は最小自乗法により求める。 |
|
|
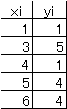
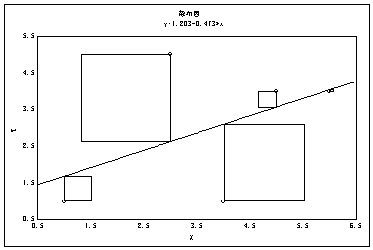
次のデータで考えてみる。yを説明するxのほかに誤差を考えて式を |
|
|
y=a+bx+誤差とする。誤差の自乗和(図4の正方形の和)を最小に |
|
|
するようにして未知係数aとbを求めるので最小自乗法とよんでいる。 |
|
|
計算は紙とエンピツでやると面倒であるが、Excelなどを用いると簡単 |
|
|
である。この例ではa=1.2、b=0.47となる。 |
|
|
|
|
|
|
|
|
|
|
|
図4で各点は〇で表している。 |
|
|
|
|
|
図4 最小自乗法の説明 |
|
|
|
|
|
最小自乗法は統計では、いろいろなところで利用されている。 |
|
|
白菜の例で単回帰式を求めると、y=51+0.6x(r=0.911)となる。つまり、 |
|
|
|
|
|
白菜漬100gの価格=51+0.6(白菜100gの価格) である。 |
|
|
|
|
|
単回帰式を表わすときは式の当てはまりがどの程度か、相関係数rも |
|
|
記載するようにしている。相関係数rは単回帰式の当てはまりのよさ |
|
|
をあらわす指標ともいえる。r=1(あるいは−1)のときはプロット |
|
|
した点がすべて直線上に並ぶ。 |
|
|
白菜の式の意味は白菜漬にすることにより、51円の付加価値を生み、 |
|
|
白菜100gの価格の6割が白菜漬にまわっていると解釈できる。 |
|
|
|
|
|
単回帰式を予測に使うことができる。たとえば、白菜100gの値段が |
|
|
10円のとき、白菜漬100gは51+0.6*10=57と予測できる。 |
|
|
|
|
|
白菜xのような変数を説明変数あるいは独立変数、白菜漬yのような |
|
|
変数を被説明変数あるいは従属変数とよんでいる。 |
|
|
|
|
1.1.3. |
散布図の重要性 |
|
|
|
|
|
Excelなどを用いれば簡単に相関係数を求めることができる。rだけの |
|
|
値から、安易に相関の有無を判定すると、判断を誤ることがある。 |
|
|
以下のデータを考える。 |
|
|
|
|
|

|
|
|
|
|
|
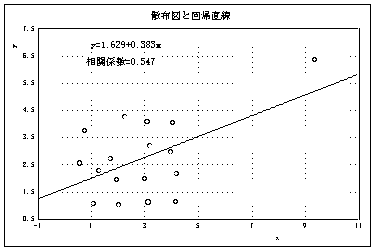
相関係数を求めると0.547である。簡便法では0.547の自乗は0.300で |
|
|
4/19=0.211より大きいので相関がありそうなのだが、念のため散布図 |
|
|
を描くと図5の上の図のようになる。右上の外れ値のために、相関が |
|
|
あるようにみえる。外れ値は測定ミスとか入力ミスによって生じる |
|
|
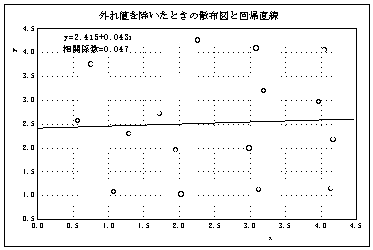
場合が少なくない。ここでは、これを(なんらかのミスによる外れ値 |
|
|
とみなして)除いて散布図を描くと下の図のようになる。相関係数は |
|
|
0.047で、相関はない。 |
|
|
逆に、図3のように相関係数が0であるからといって、xとyとに関連 |
|
|
がないと判断するのも誤りである。xとyは明らかに関連がある。この |
|
|
ように、相関係数値だけで判断するのではなく、散布図を描いてみる |
|
|
ことが重要である。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
図5 散布図の重要性を示す例 |
|
|
|
|
1.2 |
重回帰分析 |
|
|
|
|
1.2.1. |
はじめに |
|
|
|
|
|
表1のようなデータがある。このデータを用いて重回帰分析を説明する。 |
|
|
|
|
|
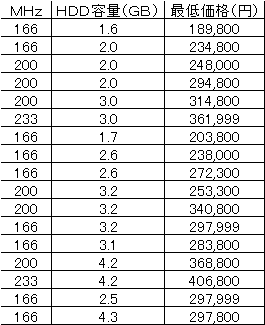
表1 ハードウェアの仕様と最低価格 |
|
|
|
|
|
「日経パソコン」97年7月14日号から |
|
|
|
|
|
最低価格をハードウェアの仕様で表す回帰式を作る。 |
|
|
まず、説明変数がMHzのときの単回帰式は |
|
|
|
|
|
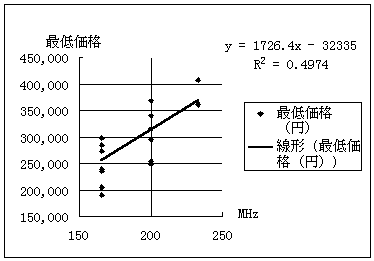
最低価格=-32,335+1,726*MHz(相関関数=0.705) (1) |
|
|
|
|
|
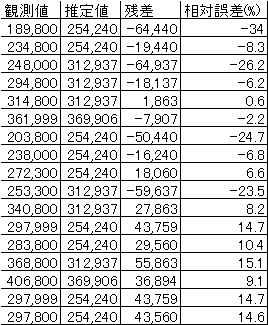
となる(図1、表2)。表2から相対誤差の絶対値の平均を求めると |
|
|
13.3%である。 |
|
|
|
|
|
|
|
|
図1 MHzと最低価格 |
|
|
|
|
|
表2 MHzを説明変数としたときの解析結果 |
|
|
|
|
|
|
|
|
また、HDDの容量(GB)を説明変数としたときは |
|
|
|
|
|
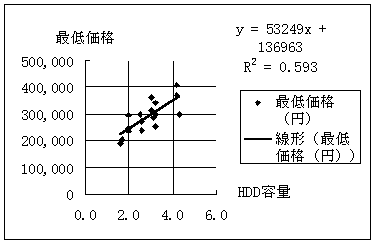
最低価格=136,963+53,249*HDD(相関係数r=0.770) (2) |
|
|
|
|
|
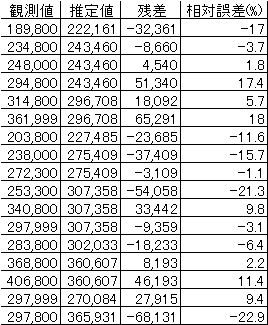
となる(図2,表3)。表3から相対誤差の絶対値の平均は10.5%である。 |
|
|
|
|
|
|
|
|
図2 HDD容量と最低価格 |
|
|
|
|
|
表3 HDD容量を説明変数としたときの解析結果 |
|
|
|
|
|
|
|
|
(1)を用いて200MHzのパソコンの最低価格を求める(予測する)と、 |
|
|
|
|
|
32,335+1,726*200=312,865円 |
|
|
|
|
|
同様に(2)を用いてHDDの容量が3GBのパソコンの最低価格を |
|
|
求めると |
|
|
|
|
|
136,963+53,249*3=296,710円 となる。 |
|
|
|
|
|
以上は各々MHz、HDD容量単独で最低価格を説明する単回帰分析である。 |
|
|
説明変数を2個以上取り扱うのが重回帰分析である。 |
|
|
|
|
|
一般に重回帰式は xi(i=1,…,k)を説明変数、y を被説明変数として、 |
|
|
|
|
|
y=a0+b1+b2+...+bk+誤差と表わす。 |
|
|
|
|
|
a0をy切片、b1,b2,…,bkを回帰係数と呼ぶ。 |
|
|
|
|
|
回帰係数は誤差の自乗和を最小にする最小自乗法を用いて求める。 |
|
|
例えば、MHzとHDD容量を同時に説明変数として重回帰式を求めると |
|
|
|
|
|
最低価格=-50,802+1,199*MHz+40,918*HDD容量(重相関係数=0.895) (3) |
|
|
|
|
|
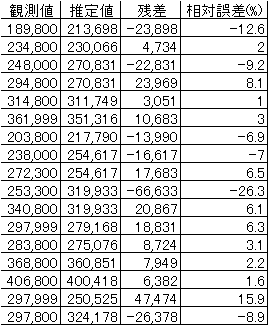
となる(表4)。 |
|
|
|
|
|
表4 MHz、HDD容量を説明変数としたときの解析結果 |
|
|
|
|
|
|
|
|
(3)を用いて200MHzでHDD容量が3GBのときの最低価格は |
|
|
311,752円となる。 |
|
|
表4から相対誤差の絶対値の平均は7.5%である。(1)のときは13.3%、 |
|
|
(2)のときは10.5%でしたから精度はよくなっている。(3)のように |
|
|
説明変数が複数個(2個以上)の式を重回帰式とか重回帰モデルとか |
|
|
とよんでいる。−50,802がy切片、1,199、40,918が回帰係数である。 |
|
|
(1)、(2)、(3)の回帰係数は最小2乗法を用いて求める。 |
|
|
重回帰式の良さを表す指標に重相関係数R がある(単回帰式のときは |
|
|
相関係数 rであった)。重相関係数は被説明変数yとyの推定値y^ |
|
|
(ワイハットと読む)との相関係数で、0<R<1である。一般にRが |
|
|
大きいほど良い回帰式といわれる。しかし、Rは、説明変数(極端な |
|
|
場合、乱数でも)をどんどん増やして、k=(データ数−1)のとき |
|
|
R=1となる。 |
|
|
|
|
|
このように、むやみに説明変数を増やしても良い回帰式が得られる |
|
|
わけではない。予測に役立つ重回帰式とはyに本当に効いている説明 |
|
|
変数だけを採用したものである。 |
|
|
したがって、最適な重回帰モデルを求めることは重回帰分析の重要な |
|
|
テーマの1つである。最適な回帰モデルを求める方法と実例について |
|
|
は上田著「データマイニング事例集」(共立出版)を参照のこと。 |
|
|
|
|
1.2.2. |
重回帰分析の目的 |
|
|
|
|
|
重回帰分析の目的には大きく分けて2つある。(1)予測と、(2)要因分析 |
|
|
である。 |
|
|
|
|
|
(1)予測 |
|
|
最適な回帰モデルが得られたとする。パソコンの例では(3)を最適な |
|
|
モデルとする。(3)を用いて233MHzで4.2GBのものは、最低価格は |
|
|
400,421円と予測できる。実際には、406,800円であったので予測の |
|
|
相対誤差は(406,800-421,400)/406,800=1.6%となる。 |
|
|
また、例えば最低価格を390,000円としたとき、HDD容量が4.2GB |
|
|
のパソコンはMHzはいくらにすべきかは、(3)から224となる。 |
|
|
|
|
|
(2)要因分析 |
|
|
被説明変数yに影響をおよぼす要因はMHzとHDD容量どちらが |
|
|
大きいだろうか。この指標(例えば貢献度指数と仮に呼ぶ)の1つに |
|
|
偏相関係数がある。これを求めると(統計ソフトを使用する。Excel |
|
|
では残念ながら求められない。)MHzは0.715、HDD容量は0.775 |
|
|
となる。簡便法による貢献度指数は回帰係数*レンジである。MHzの |
|
|
レンジを求めると、最大値(233)-最小値(166)なので、貢献度指数は |
|
|
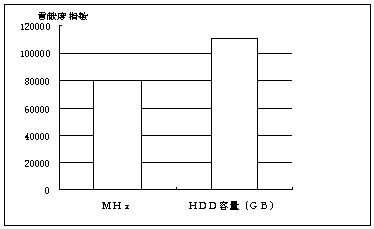
1,199*(233-166)=80,333.0、同様にHDD容量のそれは、 |
|
|
40,918*(4.3-1.6)=110,478.6となる。グラフにすると図3のようになる。 |
|
|
HDD容量のほうが最低価格に影響を及ぼしていることになる。 |
|
|
|
|
|
|
|
|
図3 貢献度指数 |
|
|
|
|
1.3 |
実験計画法 |
|
|
|
|
1.3.1. |
はじめに――実験計画法とは |
|
|
|
|
|
女性向けの1泊観光旅行を企画することを例にとりあげて説明する。 |
|
|
企画案がいろいろ出たが、旅行の行き先は奈良(古代をたずねる) |
|
|
あるいは山陰(毛利、尼子の戦国時代をたずねる)、ガイドの有無は、 |
|
|
ガイド付きあるいはガイドはなくてできるだけ自由行動時間がある、 |
|
|
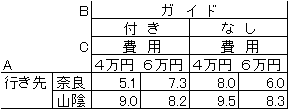
費用は4万円あるいは6万円となった。全部で23=8とおりの案ができる。 |
|
|
各案についてOL(10人程度)にアンケート形式で回答をいただいた。 |
|
|
数値は10点満点として10人の平均点を書き込んでいる。このように |
|
|
実験計画法という手法を用いて計画的にデータ(ここではアンケート) |
|
|
をとる。 |
|
|
|
|
1.3.2. |
用語の説明 |
|
|
|
|
|
A 行き先、B ガイドの有無、C 費用を要因(あるいは因子)とよぶ。 |
|
|
例では3つの要因があるわけである。行き先は奈良あるいは山陰2つ |
|
|
ある。これを水準とよんでいる。ガイドも2水準、費用も2水準で |
|
|
ある。得られた回答結果を特性値とよぶ。要因が3つで、上のような |
|
|
表を作って実験(ここではアンケート)を行うので3元配置実験と |
|
|
いう(要因が4つのときは4元配置実験という)。実験計画法とは |
|
|
特性値に影響を及ぼしている要因をみつけ、かつその要因のどの水準 |
|
|
のとき特性値が最大(あるいは場合によっては最小)になるかを推定 |
|
|
する手法である。 |
|
|
この例では、回答者の満足度を高める要因と水準をみつけることになる。 |
|
|
|
|
|
表1 OL向け1泊観光旅行案と回答結果 |
|
|
|
|
|
|
|
1.3.3. |
直交表を利用する |
|
|
|
|
|
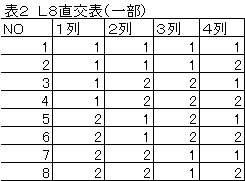
表2はL8直交表と呼ばれるものの一部である。1と-2があるルールに |
|
|
したがって、規則正しく並んでいる。直交表にはL8のほかL4、L16、L32、 |
|
|
L64、L9、L27、L81とかがある。 |
|
|
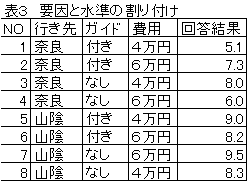
この表の1,2,4列を利用して表3を作る。1を第1水準に−1を |
|
|
第2水準に対応させている。さらにアンケート結果を右端に記入した。 |
|
|
この直交表の相関係数を求めると表4のように相関係数がすべて0に |
|
|
なっている。直交表とは要因内の水準の組み合わせを公平にして相関 |
|
|
係数がすべて(自分自身は1である)0になるようにしたものである。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
さて、要因としてさらに交通手段を考えたとする。水準1はジェット機 |
|
|
とバス、水準2は新幹線+在来線とバスである。すると、要因は4つ |
|
|
であるからすべての組み合わせは16とおりになる。しかしながら、 |
|
|
直交表を使うとその半分の8とおりでおさまる。直交表は実験回数が |
|
|
少なくてすむように配慮して作成されているところに特徴がある。 |
|
|
実験計画法は最小の実験回数で最大の情報を得る、うまく、はやく、 |
|
|
やすくを実現した画期的な手法である。実験計画法のデータの解析は、 |
|
|
伝統的には分散分析法を用いる。つまり、分散分析表を求め、注目 |
|
|
している要因が有意かどうかを(F検定により)判定する。 |
|
|
|
|
|
|
|
1.3.4. |
データを解析する |
|
|
|
|
|
ここでは、実験計画法データを分散分析でなく、回帰モデルを用いて |
|
|
解析する方法をとる。それを説明する。 |
|
|
3つの要因の場合の回帰分析モデルのデータを作ると表5のようになる。 |
|
|
表5をよく見ると、数量化理論1類モデルと数学モデルでは同一である |
|
|
ことがわかる。このデータをExcelの関数「回帰分析」で解いて回帰係数を |
|
|
求める。この回帰係数(表5)が行き先奈良、ガイド付き、費用4万円 |
|
|
の各満足度となる。 |
|
|
|
|
|

|
|
|
|
|
|

|
|
|
|
|
|
満足度は次のように表わせる。 |
|
|
|
|
|
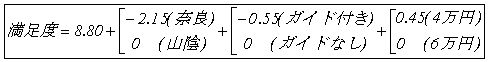
|
|
|
|
|
|
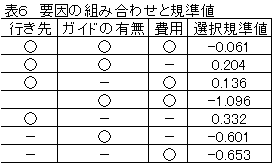
特性値(y)に影響を及ぼしている要因を見つけるには、要因(変数) |
|
|
選択規準を使う。表6は各要因を選択したときの選択規準の値である。 |
|
|
|
|
|
|
|
|
|
|
|
要因選択規準が最大となっているのは要因が行き先1つのときである。 |
|
|
効いている要因は行き先のみであることがわかる。ガイドの有無と |
|
|
費用は重要視していないということである。 |
|
|
旅行会社の立場では、費用をおさえて、売上げを多くするには、 |
|
|
行き先は山陰、ガイドなしで、費用は6万円のコースが良いことになる。 |
|
|
|
|
|
行き先のみを用いた回帰式は |
|
|
|
|
|
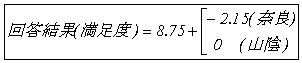 となる。 となる。
|
|
|
|
|
|
この式から、奈良と山陰では山陰の方が好まれ、山陰と奈良では、2.15 |
|
|
の差があり、奈良を選んだときの満足度は8.75−2.15=6.60,山陰の |
|
|
ときは8.75と推定できる。 |
|
|
|
|
|
まとめると次のようになる。 |
|
|
直交表など、実験計画法にしたがいデータを効率良く得ることが大切 |
|
|
である。得られたデータを解析して、特性値に影響を及ぼしている |
|
|
要因を求めるには、回帰モデルを作り、変数選択規準を用いる。 |
|
|
回帰係数を用いて要因分析、予測(推定)を行う。 |
|
|
(注)変数選択基準Ruとは |
|
|
Ru=1-(1-重相関係数の2乗)*(データ数+説明変数の個数+1)/(データ数-説明変数の個数-1) |
|
|
である。 |
|
|
Ruが最大の変数の組み合わせを選択する。ここでは、説明変数の個数 |
|
|
は、注目している要因の水準数−1の和となる。 |
|
|
|
|
|
<補足>2元配置実験データの場合 |
|
|
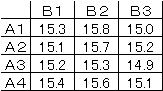
要因A,Bがあり、Aは4水準、Bは3水準をとるものとする。例えば |
|
|
Aは温度、Bは気圧とする。次のようなデータ(生成物(y)とする)が |
|
|
得られたとする。 |
|
|
|
|
|
|
|
|
(注)このような実験を2因子実験とか2元配置実験と呼ぶ。 |
|
|
|
|
|
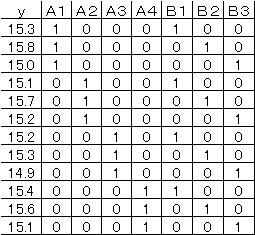
これを回帰分析可能なデータに書き直すと次のようになる。 |
|
|
|
|
|
|
|
|
|
|
|
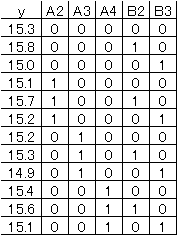
さらに、実行可能なデータはA1列とB1列を削除して、以下のようになる。 |
|
|
|
|
|
|
|
|
|
|
|
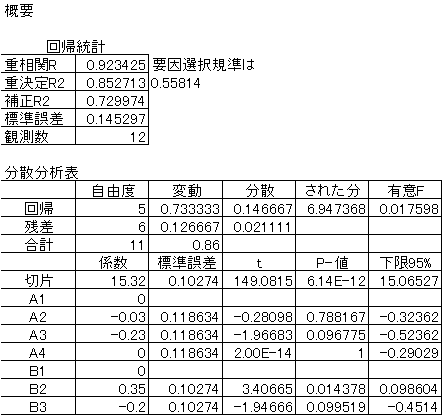
実行結果は下のようになる。A1列とB1列を削除したので、A1と |
|
|
B1の回帰係数を0とした。 |
|
|
|
|
|
|
|
|
|
|
|
(注)説明変数x1〜x7を用いて回帰式をあらわすと、 |
|
|
y=15.32+0.00x1-0.03x2-0.23x3+0.00x4-0.00x5+0.35x6-0.20x7 |
|
|
となる。 |
|
|
A1〜A4,B1〜B3を用いてあらわすと、 |
|
|
|
|
|
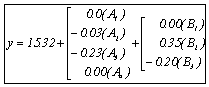 (1) (1)
|
|
|
|
|
|
要因選択規準は0.558となった。 |
|
|
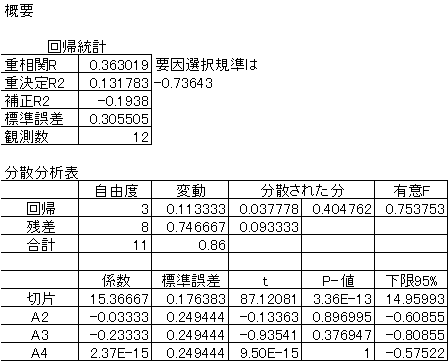
要因Aのみを用いた回帰分析の実行結果は以下のようになる。 |
|
|
|
|
|
|
|
|
|
|
|
回帰式は、 |
|
|
|
|
|
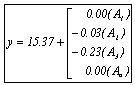 (2) (2)
|
|
|
|
|
|
となる。 |
|
|
要因選択規準は-0.736となった。 |
|
|
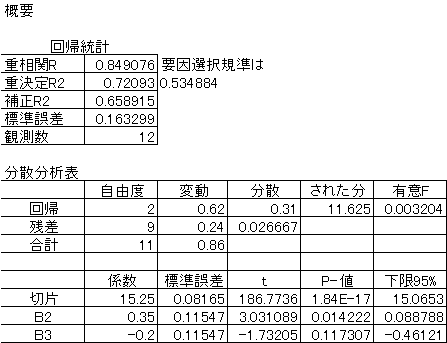
要因Bのみを用いた回帰分析の実行結果は以下のようになる。 |
|
|
|
|
|
|
|
|
|
|
|
回帰式は、 |
|
|
|
|
|
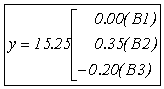 (3) (3)
|
|
|
|
|
|
となる。 |
|
|
要因選択規準は0.535となった。要因と要因選択規準をまとめると |
|
|
次のようになる。 |
|
|
|
|
|

|
|
|
|
|
|
したがって、要因A,Bともに効いていることになる。 |
|
|
(1)式より、特性値yを最大にするには、要因Aは第1水準あるいは |
|
|
第4水準、要因Bは第2水準をとればよいこたがわかる。このとき、 |
|
|
y=15.32+0.00+0.35=15.67となる。 |
|
|
|
|
1.4 |
直交表とは |
|
|
|
|
1.4.1. |
直交とは |
|
|
|
|
|
直交表の直交とは何を意味するのであろうか。例えば、L4直交表は |
|
|
次のようになっている。 |
|
|
|
|
|
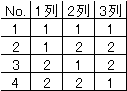
|
|
|
|
|
|
で2を−1におきかえると次のようになる |
|
|
|
|
|
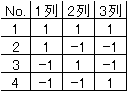
|
|
|
|
|
|
1列と2列の積和を考えると、1*1+1*(-1)+(-1)*1+(-1)*(-1)=1-1-1+1=0 |
|
|
となる。1列と3列の積和も、1*1+1*(-1)+(-1)*(-1)+(-1)+1=1-1+1-1=0 |
|
|
となる。2列と3列の積和も0となる。 |
|
|
どの列の積和をとっても0となるので直交表と呼ばれる。 |
|
|
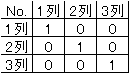
相関係数を求めると、次のようになる。 |
|
|
|
|
|
|
|
|
|
|
|
自分自身の相関係数は1となり、他の列との相関係数はすべて0と |
|
|
なっている。 |
|
|
他の直交表(L8 L16 L32 L64 L9 L27 L81 L12 L18 L36 |
|
|
など)について相関係数を求めると、すべて単位行列(対角要素が |
|
|
1で他はすべて0の行列)になっている。 |
|
|
|
|
|
(注)直交表をデータとみなして相関係数を求めると単位行列になる |
|
|
が、単位行列になるものは直交表とは限らない。 |
|
|
|
|
1.4.2. |
L8直交表 |
|
|
|
|
|
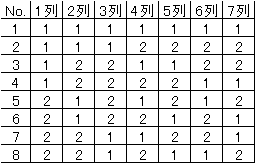
L8直交表を考える。L8の8は8回に実験を行うことを示す。最大 |
|
|
7つの要因を割りつけることができる。 |
|
|
|
|
|
|
|
|
|
|
|
1列に要因Aを2列にBを……、7列にGを割りつけると、No.1の |
|
|
実験はA〜Gまですべて第1水準ということになる(これをA1〜G1 |
|
|
と表す)。また、No.5の実験は、A2 B1 C2 D1 E2 F1 G2となる。 |
|
|
|
|
|
|
|
|
|
|
|
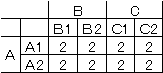
AとBの実験の組み合わせは、A1 B1〜A2 B2すべて2回、AとC |
|
|
の実験の組み合わせは、A1 C1〜A2 C2すべて2回となることがわかる。 |
|
|
回数はバランスよく、公平に実験を行うことになる。 |
|
|
|
|
|
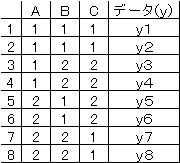
L8直交表実験データの解析はどのようにするのであろうか。実験計画法 |
|
|
では分散分析法による。本書では回帰分析法による。1列にA、2列にB |
|
|
、3列にCを割りつけて実験を行い、下のようなデータとなったとする。 |
|
|
|
|
|
|
|
|
|
|
|
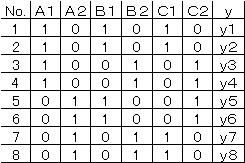
回帰分析法では次のように書き直す。 |
|
|
|
|
|
|
|
|
|
|
|
y1のデータはAはA1、BはB1、CはC1のときであるから、該当して |
|
|
いる所へ1、そうでなければ0を記入する。 |
|
|
y4のデータはA1,B2,C2であるから4行目は1,0,0,1,0,1と |
|
|
する。その他の行も同様にして作る。 |
|
|
Excelの回帰分析で実行するときは、数学的な理由から各要因の列データ |
|
|
を1列ずつ削除する必要がある。 |
|
|
|
|
|
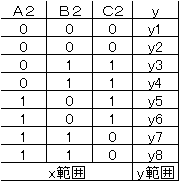
したがって、実行可能な形は次のようになる。 |
|
|
|
|
|
|
|
|
|
|
|
回帰分析を実行し、回帰係数が各要因の水準の効果の大きさとなる。 |
|
|
削除したA1 B1 C1の回帰係数は0とする。 |
|
|
|
|
1.4.3. |
直交表 |
|
|
|
|
|
直交表には以下のようなものがある。 |
|
|
|
|
|

|
|
|
|
|
|
品質工学でよく使用されるものにはL12 L18 L36がある。 |
|
|
|
|
1.4.4. |
直交表を回帰分析用に直す |
|
|
|
|
|
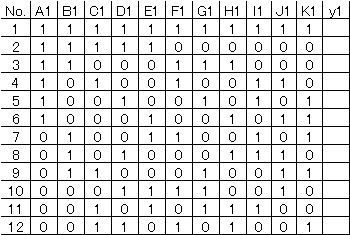
L12のExcelの回帰分析用は次のようになる。 |
|
|
|
|
|
|
|
|
(注)各要因(因子)の第1水準(列)を削除してある。 |
|
|
yに特性値データをインプットして回帰分析を実行すればよい。 |
|
|
|
|
|
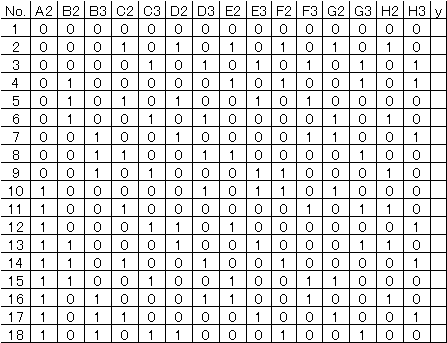
L18のExcelの回帰分析用は次のようになる。 |
|
|
|
|
|
|
|
|
(注)各要因(因子)の第1水準(列)を削除してある。 |
|
|
yに特性値データをインプットして回帰分析を実行すればよい。 |
|
|
|
|
1.4.5. |
新しい直交表を作る例 |
|
|
|
|
|
L18直交表は2水準と3水準の要因しか割り付けられない。たとえば、 |
|
|
6水準の要因があるときはどうすればよいのであろうか。次のように |
|
|
して6水準の要因(因子)を作る。 |
|
|
|
|
|
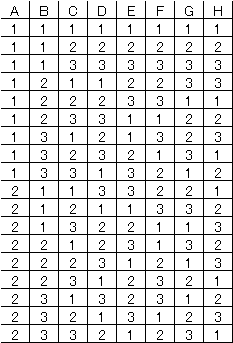
L18直交表で6水準の因子を作る |
|
|
|
|
|
|
|
|
|
|
|
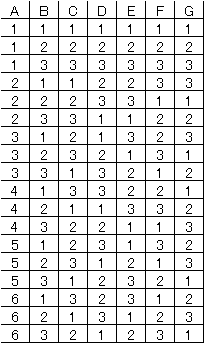
AとBで(11)を1,(12)を2,(13)を3,(21)を4,(22)を5,(23) |
|
|
を6をとすると6水準の因子列ができる。 |
|
|
|
|
|
|
|
|
|
|
1.4.6. |
いろいろな直交表 |
|
|
|
|
|
いろいろな直交表と相関係数を載せるので実務に役立てていただきたい。 |
|
|
|
|
|
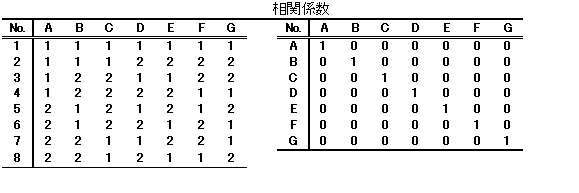
(1) L8直交表2222222(8):2水準が7個,実験回数が8回 |
|
|
|
|
|
|
|
|
|
|
|
(2) L12直交表22222222222(12):2水準が11個,実験回数が12回 |
|
|
|
|
|

|
|
|
|
|
|
(3) L16の直交表:2水準が15個,実験回数が16回 |
|
|
|
|
|

|
|
|
|
|
|
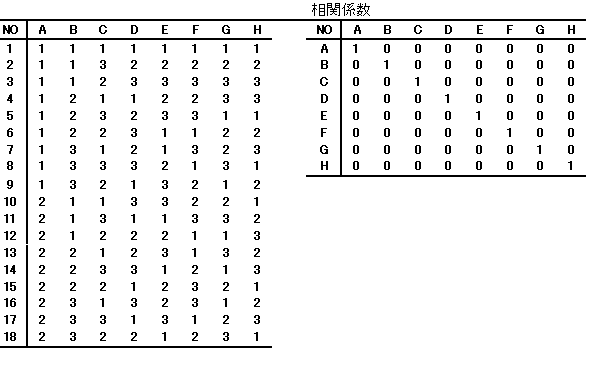
(4) L18の直交表:左から2,3,3,3,3,3,3水準、実験回数が18回 |
|
|
|
|
|
|
|
|
|
|
|
(5) L27の直交表:3水準が13個,実験回数が27回 |
|
|
|
|
|

|
|
|
|
|
|
(6) L18の直交表6333333(18):左から6,3,3,3,3,3,3水準、実験回数が18回 |
|
|
|
|
|

|
|
|
|
|
|
(7) L36の直交表 |
|
|
|
|
|

|












